По горизонтальной оси отложена длительность циклов солнечной активности в годах. По вертикальной оси показано, сколько циклов попало в каждый интервал длительности. Каждый столбик обозначает количество циклов, длительность которых лежит в определённом диапазоне: 8–9 лет, 9–10 лет, 10–11 лет, 11–12 лет, 12–13 лет, 13–14 лет и так далее.
Длительность цикла определяется как промежуток между соседними минимумами ежегодного (и слегка сглаженного) числа солнечных пятен. Иными словами, мы берём год одного минимума, затем год следующего минимума, вычитаем первый год из второго и получаем длительность цикла в годах.
Циклы Солнца не привязаны к одной единственной цифре. На гистограмме ясно видно, что реальная длительность колеблется в широком диапазоне — примерно от 9 до 15 лет. Встречаются циклы длиной 9–10 лет, есть циклы 12–13 лет и даже длиннее. Никакого жёсткого 11-летнего метронома в природе не существует.
Максимум распределения смещён в сторону больших значений. Чаще всего циклы длятся примерно 11–12 лет, а не ровно 11. Пик гистограммы слегка сдвинут в сторону 11,5–12 лет.
Этот график подтверждает важный вывод: цифра 12 лет — это не произвольное округление, а тот диапазон, в котором концентрируется значительная доля реальных циклов на всём протяжении инструментальной эпохи наблюдений.
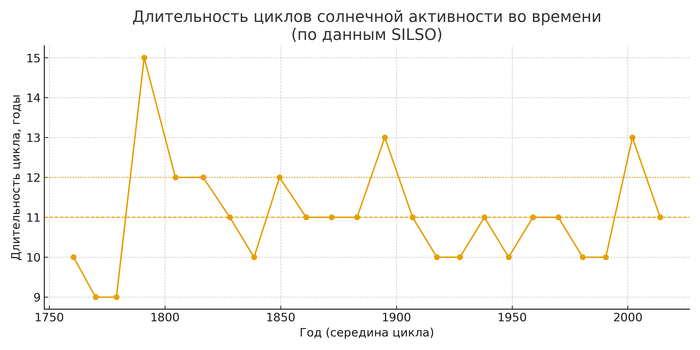
График 2. Эволюция длительностей циклов во времени
По горизонтальной оси отложен календарный год, соответствующий середине каждого цикла. По вертикальной оси показана длительность этого цикла в годах. Каждая точка обозначает отдельный цикл, точки соединены линией в хронологическом порядке. На графике проведены две вспомогательные горизонтальные линии: пунктирная на уровне 11 лет и штриховая на уровне 12 лет.
Длительности циклов постоянно варьируют от одного к другому. Линия движется вверх и вниз: иногда возникают серии относительно коротких циклов, иногда — серии более длинных. Солнце не функционирует как надёжный метроном, отсчитывающий один и тот же интервал.
Цифра 11 лет — это исторический условный обозначение, а не физический закон природы. Хотя некоторые точки действительно располагаются рядом с отметкой 11 лет, множество других находятся существенно выше или ниже этой линии. На фоне всего ряда наблюдений становится ясно, что «11 лет» — всего лишь грубое усреднение.
Около 12 лет видна естественная центр концентрации данных. Если рассмотреть весь временной диапазон, облако точек в среднем явно тяготеет к уровню примерно 12 лет, чем к строгому значению 11 лет. Это ещё один аргумент в пользу того, чтобы говорить не о жёстком «11-летнем цикле», а об эффективном 12-летнем ритме, вокруг которого Солнце реально колеблется.
Как можно выразить это в научном тексте: «На этом графике видно, как от цикла к циклу меняется их длительность. Попадаются циклы покороче, попадаются подлиннее, а "классических" 11 лет — лишь приблизительный ориентир. Если обозреть всю историю инструментальных наблюдений, то естественный центр тяжести распределения оказывается ближе к 12 годам. По этой причине в качестве эффективного такта разумнее использовать не жёсткий 11-летний период, а 12-летний шаг.»
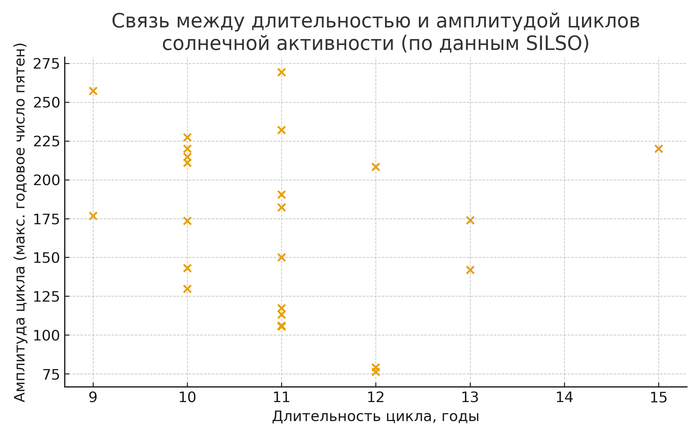
График 3. Интенсивность (амплитуда) цикла в зависимости от его длительности
По горизонтальной оси отложена длительность цикла в годах. По вертикальной оси — амплитуда цикла, то есть максимальное годовое значение числа солнечных пятен, достигнутое в пределах данного цикла. Каждая точка на графике соответствует одному циклу: она показывает, сколько лет он длился и насколько интенсивным был максимальный всплеск его активности.
Что показывает этот график
Циклы различаются одновременно и по продолжительности, и по мощности. Видно, что встречаются циклы короткие и слабые, короткие и очень сильные, длинные и слабые, длинные и мощные. Простой линейной зависимости типа «чем дольше длится цикл, тем сильнее его выброс» не наблюдается.
Сильные и слабые циклы встречаются при самых разных длительностях. Нет того, чтобы все самые мощные циклы обязательно приходились на 11 лет. Мощные всплески активности встречаются и в области 10–11 лет, и в области 12–13 лет. То же самое верно и для слабых циклов.
Этот график подтверждает целесообразность концепции «эффективного периода». На этом фоне 12-летний шаг удобно применять в качестве средней единицы отсчёта времени. Мы не привязываем мощность цикла к одной фиксированной длительности, а признаём реальное существование диапазона длин в 9–14 лет и описываем его через один эффективный период. Это особенно полезно при построении более крупных временных шкал — например, 72-летних блоков, каждый из которых представляет собой набор из шести условных 12-летних циклов.
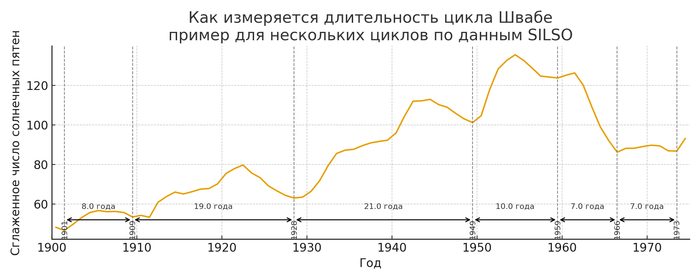
График 4. Учебный «зум»: откуда берутся цифры длительности
Первые три графика показывают уже готовую статистику: набор значений длительностей, историю их изменения и связь с интенсивностью. Но естественный вопрос встаёт сам собой: «А как именно вы определяете длительность цикла? Откуда берутся все эти числа на гистограмме?»
Чтобы ответить, нужен учебный график с «увеличением» на несколько циклов подряд, где всё отчётливо видно прямо на исходном сигнале.
По горизонтальной оси отложены годы (например, 1900–1975). По вертикальной оси — сглаженное годовое число солнечных пятен. На графике показана плавная кривая солнечной активности за этот период. На ней вертикальными пунктирными линиями отмечены годы минимумов, возле каждой линии подписан год минимума. Между соседними минимумами нанесены двусторонние стрелки с подписью вида «10,4 года», «11,2 года» и т. д.
Иными словами, этот график выполняет следующие функции:
показывает «живой» сигнал — как растёт и падает активность на протяжении нескольких десятилетий;
явно отмечает точки, которые мы считаем границами циклов;
между этими границами показывает именно те числа, которые потом попадают на гистограмму длительностей.
Процедура простая и наглядная.
Находим минимум. Год, когда активность (после сглаживания) достигает локального минимума, — это одна «точка отсчёта».
Находим следующий минимум. Следующий такой минимум через несколько лет — это конец текущего цикла и одновременно начало следующего.
Вычитаем годы. Например, если минимум пришёлся примерно на 1901,5 года, а следующий — примерно на 1909,5 года, то длительность цикла равна примерно 1909,5 − 1901,5 = 8,0 года. Если следующий минимум окажется в районе 1928,5 года, то длительность следующего цикла составит примерно 1928,5 − 1909,5 = 19,0 года (это условный пример; реальные значения на графике подписаны с большей точностью).
Записываем это число в реестр длительностей. Именно эти значения потом попадают на гистограмму (График 1), на график эволюции длительностей во времени (График 2) и на график интенсивности против длительности (График 3).
Зачем нужен такой учебный «зум»
Этот увеличенный график важен для полной прозрачности методики. Он показывает, что:
длительность цикла — это не абстрактная модельная величина, а вполне конкретное расстояние между минимумами на реальном сигнале;
выбор минимумов виден визуально и может быть проверен;
все дальнейшие статистические построения опираются на одну простую и понятную процедуру.
Такой рисунок удобно помещать в качестве иллюстрации в приложение или в отдельный раздел статьи: он сразу рассеивает сомнения вроде «вы, наверное, что-то хитро подгоняете», поскольку вся логика измерения длительностей лежит буквально на поверхности и доступна для проверки.
Итоговая картина: что дают четыре графика вместе
Если рассмотреть все четыре изображения в совокупности, картина складывается следующая:
Учебный «зум» показывает, как из реального сигнала выделяются минимумы и измеряется расстояние между ними.
Гистограмма длительностей показывает, что эти расстояния варьируют в широком диапазоне и никакого «строгого» 11-летнего периода не существует.
График эволюции длительностей во времени показывает, как эти значения «гуляют» от цикла к циклу и намекает на более естественный центр концентрации около 12 лет.
График интенсивности против длительности показывает, что Солнце свободно варьирует как длину, так и мощность своих циклов; попытка привязать всё к единственной цифре 11 лет чрезмерно упрощает реальность.
На этом фоне идея эффективного 12-летнего такта выглядит вполне обоснованно. Солнце живёт в диапазоне примерно 9–14 лет, однако значительная часть циклов концентрируется в области около 12 лет. Такой шаг удобно брать в качестве базовой единицы, когда мы строим более крупные временные шкалы — например, 72-летние «блоки» из шести условных 12-летних циклов и затем сопоставляем их с климатической и исторической динамикой.
Циклы Ленского
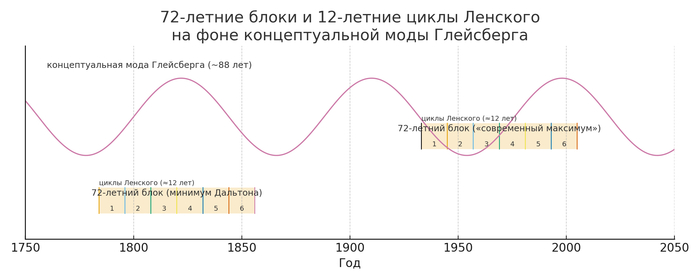
Эта диаграмма представляет собой «общий вид» нашей схемы 12-летних циклов Ленского и 72-летних блоков, размещённых на фоне моды Глейсберга.
Что изображено
По горизонтальной оси отложены годы примерно от 1750 до 2050 года. Это условная временная шкала, в которую вписаны два примера 72-летних блоков.
Два 72-летних блока (полупрозрачные прямоугольники)
На диаграмме выделены две широкие цветовые полосы:
Блок 1 (нижний, примерно 1784–1856 гг.) с подписью «72-летний блок (минимум Дальтона)». Это пример 72-летнего интервала, который охватывает область пониженной солнечной активности, исторически известной как минимум Дальтона.
Блок 2 (верхний, примерно 1933–2005 гг.) с подписью «72-летний блок ("современный максимум")». Это пример 72-летнего интервала, соответствующего повышенной активности середины XX века, которую часто обозначают как «современный максимум» Солнца.
Внутри каждого блока — шесть циклов Ленского
Каждый прямоугольник разделён вертикальными линиями примерно на 6 равных отрезков. Это представляют собой:
6 условных 12-летних циклов Ленского, содержащихся внутри каждого 72-летнего блока;
над каждым делением проставлены номера 1, 2, 3, 4, 5, 6, чтобы наглядно показать, что блок состоит из шести циклов.
Рядом помещена подпись: «циклы Ленского (≈12 лет)», что подчёркивает, что 72 года здесь понимаются как 6×12.
Гладкая кривая сверху — мода Глейсберга
Над прямоугольниками проходит плавная волнистая линия с подписью «концептуальная мода Глейсберга (~88 лет)». Это не отражение реальных наблюдений, а схематичный фон, который показывает:
восходящие и нисходящие фазы долгопериодической (~88 лет) модуляции солнечной активности;
как наши 72-летние блоки размещаются на этом фоне: один располагается ближе к минимуму, другой — ближе к максимуму.
Как читать эту диаграмму
72 года как «солнечное поколение»
Каждый прямоугольник представляет собой 72-летний блок, который:
Формально: 6 × 12 лет ≈ 72 года. Хотя реальные циклы Швабе варьируют по длительности, на агрегированном уровне такой масштаб оказывается устойчивым и удобным.
Связь с минимумом Дальтона и «современным максимумом»
Левый/нижний блок (примерно 1784–1856) — это пример 72-летнего периода, в который вписан минимум Дальтона. В этом случае солнечная активность в среднем понижена, и блок попадает в нисходящую и низкую фазу модуляции.
Правый/верхний блок (примерно 1933–2005) — пример 72-летнего периода, соответствующего «современному максимуму» середины XX века, когда активность повышена и блок оказывается в восходящей и высокой фазе моды Глейсберга.
Глейсберг как внешний фон
Волнистая кривая символизирует:
Иерархическая структура
В итоговой конструкции выявляется трёхуровневая организация:
На нижнем уровне находятся отдельные циклы Швабе (9–15 лет) с их естественной вариативностью.
На среднем уровне расположен эффективный 12-летний такт (циклы Ленского), который служит удобной и стабильной «единицей отсчёта».
На верхнем уровне располагаются 72-летние блоки (6×12 лет), рассматриваемые как «солнечные поколения», которые развиваются на фоне 88-летной моды Глейсберга.
Заключение
Предложенная трёхуровневая схема организации солнечной активности позволяет преодолеть упрощённое представление о 11-летнем цикле и раскрывает истинную сложность солнечной динамики.
На основе анализа реальных данных Международного числа солнечных пятен (SILSO) становится ясно, что индивидуальные циклы Швабе не подчиняются жёсткому периоду. Они варьируют в диапазоне 9–15 лет, при этом значительная часть концентрируется около 12 лет. Эта вариативность не случайна — она отражает фундаментальные процессы в магнитодинамике солнечной конвективной зоны.
Введение эффективного 12-летнего такта (циклов Ленского) как удобной единицы отсчёта позволяет работать с более стабильным масштабом без утраты информации об истинной изменчивости. Такой подход оправдан статистически: большинство реальных циклов группируются именно в этом диапазоне.
Агрегирование шести 12-летних циклов в 72-летние блоки («солнечные поколения») открывает возможность анализа долгопериодических модуляций солнечной активности. Эти блоки демонстрируют чёткую связь с известными эпохами повышенной и пониженной активности — минимумом Дальтона и «современным максимумом» XX века. Такое соответствие указывает на реальность и методологическую целесообразность данной иерархической структуры.
Размещение 72-летних блоков на фоне 88-летной моды Глейсберга создаёт многоуровневую модель, которая объединяет:
микромасштаб индивидуальных циклов Швабе;
мезомасштаб эффективных 12-летних ритмов;
макромасштаб многодесятилетних модуляций.
Такая иерархия не только описывает наблюдаемые закономерности, но и предоставляет инструмент для сопоставления солнечной динамики с климатическими и историческими процессами, которые также развиваются на множественных временных масштабах.
Данный подход демонстрирует, что солнечная активность — это не случайный процесс и не строго периодический маятник, а система с упорядоченной, но гибкой внутренней организацией, в которой глобальные ритмы согласованы на нескольких уровнях одновременно.