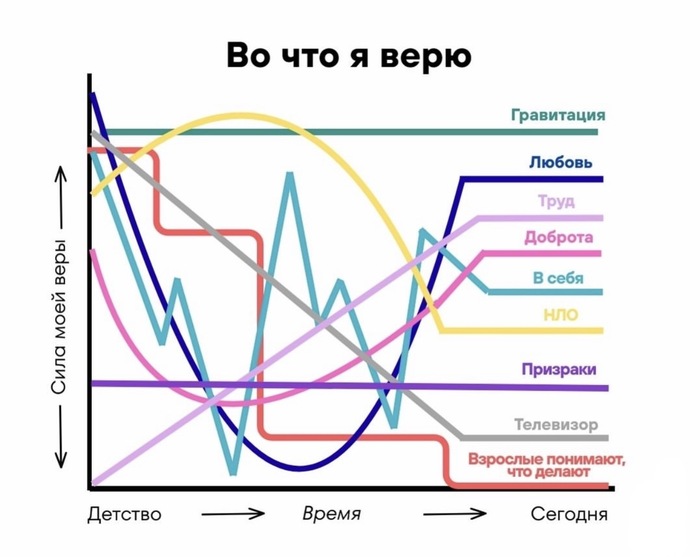
Вращение, гравитационное поле и климат Земли. Леонид Зотов
Земля ускоряется. В 2024 году зафиксированы рекорды скорости вращения. Пропало Чандлеровское колебание полюса. Спутники GRACE видят, как перераспределяются массы планеты. Что происходит и как это связано с климатом? Леонид Зотов — учёный, исследователь вращения Земли — объясняет, почему планета сжата с полюсов, как работают гравиметры, зачем нужна добавочная секунда и при чём тут лунные циклы. От Ньютона и Ковалевской до глобального потепления и многолетнего атлантического колебания.
⏱️ Таймкоды в видео:
0:00 — Вступление, конференция «Математика добра»
1:12 — Что вращается во Вселенной
4:04 — Коперник и системы мира
8:31 — Математика вращения: Пуанкаре, Ковалевская
10:07 — Ньютон и законы механики
16:44 — Угловая скорость и гироскопы
23:45 — Почему Земля сжата с полюсов
31:45 — Гравиметры: как измеряют силу тяжести
34:48 — Спутники GRACE: мониторинг массы Земли
39:00 — Сила Кориолиса и маятник Фуко
43:29 — Прецессия земной оси и ледниковые периоды
48:57 — Движение полюса Земли за 150 лет
57:01 — Почему Земля ускоряется? Рекорды 2024 года
1:07:13 — Проблема добавочной секунды
1:10:12 — Глобальное потепление и уровень моря
1:24:22 — Многолетнее атлантическое колебание (90 лет)
1:33:40 — Гипотеза: лунные циклы и климат
1:38:25 — Фонд «Детские деревни SOS» Лекция в рамках благотворительной конференции «Математика добра».
Леонид выбрал фонд «Детские деревни SOS» — помощь детям, оставшимся без родителей: https://sos-dd.ru/
Telegram (анонсы и розыгрыши): https://t.me/mathloversclub28
Подробнее о конференции (расписание и бонусы): https://www.notion.so/mathloversclub/2025-2ce28c0e8517819882...
Все записи конференции — в нашем профиле на Stepik: https://stepik.org/users/645988571/teach #вращениеЗемли #климат #геофизика #астрономия #научпоп
Теория Эфира и Теория Относительности. 120 лет. Куда катится Мир
Какая из двух - теория заговора?
Эфирная теория под запретом на научном или официальном уровне.
У эфирное теории (гравитации) есть маленький "недостаток". Она хоть и объясняет ВСЁ (и даже то что не может Т.О. Эйнштейна объяснить), но у нее нет простой "подачи", "картинки", "обёртки" для массового читателя (покупателя), например как в магазине для товара нужна красивая броская упаковка, если нужно чтоб он хорошо продавался.
Эйнштейн, как известно, взял за основу своей теории эфирную теорию (он сам это прямо пишет в своих работах), и значит, все формулы вывел на основе существования эфира, или "не пустого энергетического поля (пространства)". Но, не создав саму модель эфира, или какой-никакой "механики" гравитации, вытекающей из свойств эфира, Эйнштейн заменил эфир и вместе с ним все неизученные свойства материи и взаимодействий, на вполне простую, достаточно красивую и "почти понятную" модель-"обёртку", "упаковав" все свои выводы и формулы в модель "кривого пространства-времени", да еще и с "приложением-картинкой" в виде провисшей под весом тяжелого шара простыни. Кто тут скажет, что простынь-пространство не прогнулась, не искривилась? Мало кто. Кто скажет что король - голый? Мало кто. Разве что, несколько смелых учёных-физиков, и какая-то часть общества, имеющая аналитическое или критическое мышление, и не боящаяся его высказывать.
В результате такой подмены понятий, теория Эйнштейна, хоть и при правильных (но не всегда и не везде) формулах, не отвечает на следующие вопросы (а эфир же - отвечает, просто и логично):
- не объясняет расширение Вселенной (эфир же расширяется почти априори, так как эфир это энергия, не имеющая “замка”, то есть связывающих сил, которые бы удерживали кластер эфира от “расширения” (раздувания как воздушный резиновый шарик)
- не объясняет гравитацию (модель “кривого” пространства - "простыни с шаром на ней" не есть объяснение, так как не приведена (искомая) причина искривления. Это просто картинка "для верующих", ставшая уже "иконой" Теории Относительности Эйнштейна)
- не объясняет тёмную материю и тёмную энергию (эфир - “объясняет”, так как это всё и есть эфир)
- не объясняет наличие гало “массы” у галактик (и не видит этого “гало” вообще у всех тел)
- не объясняет эффект замедления времени (как и с гравитацией, “объясняется” - снова “искривлением”, без причин. Просто - верить? “Математика же”! “Числа всё объясняют” (примерно такие есть выражения у сторонников Т.О.)
- постоянство скорости света определено как постулат, а не как известный и понятный природный факт (распространение волн в среде), который надо дальше изучать и правильно применять
- не даёт объяснения природе распространения света (ЭМВ), не связывает никаким механизмом пространство и составляющие и наполняющие его колебания
- не даёт объяснения эффекту наличия при некоторых условиях скорости, большей скорости света, создав для устранения этого факта неуклюжую “обманку” - так называемое “кажущееся сокращение длины” объекта при больших скоростях. Вообще, в точных науках, слова “кажется” - как минимум, странно звучит, если говорить дипломатично или без сарказма.
- не даёт своего объяснения гравитационному линзированию, и другим явлениям, которые концепция эфира (или по-другому - не пустого энергетического пространства) -легко и просто объясняет и даже без формул, просто логикой и накопленным научным опытом.
- не даёт объединения теории гравитации с квантовыми механизмами, не объединяет макро-и микро -процессы. Эфир с квантовой теорией - согласуется, и взаимодействуют на квантовом уровне.
Итак, Т,О, Эйнштейна, основана на теории эфира, и показывает, или предсказывает далеко не все явления, обнаруженные или открытые за более 100 лет, многого не объясняет и не приближается к объяснению.
Слова самого Эйнштейна: “теория (Т.О,) нуждается в доработке”. “Доработка” может вылиться в полное переосмысление или даже отказ от неё. И похоже, что все к этому движемся. Например, понятие “пустого пространства” начинает заменяться энергетическим “полем Хиггса”. Это - по сути, сдача “позиций”. Уже можно сказать что это и есть эфир (почти).
Дальше, с годами, можно ожидать что поле “Хиггса” обладает массой, и состоит оно из квантов-кластеров с массой и упругостью. Что они, эти кластеры - “гравитоны-ньютонии-амеры и т.д.”, могут возбуждаться от квантовых и атомных процессов и переносить возбуждение из атома в среду эфира, создавая таким образом электромагнитную волну, скорость которой определяется не скоростью движения атома, а только условиями среды.
Далее, “обнаружится”, что каждый кластер-гравитон обладает не связанной ни с чем энергией (или почти не связанной), поэтому от расширяется, выдавливая “наружу” всё вокруг себя - и соседние такие же “кластеры-ячейки”, и не далеко находящиеся частицы вещества.
Дальше - еще проще. Причина гравитации, и всех связанных с ней “парадоксальных явлений” будет видна и понятна всем, и даже школьникам, как например понятно почему корабли в волнительном море “притягиваются”, или дым от костра даже при ветре может тянуться к человеку если он рядом.
Резюме.
Теория Эфира, в отличие от Теории Относительности (Специальной и Общей), не обладает нужной “продающей картинкой”, “рекламным образом”, коротко и просто объясняющими суть теории, по этой причине и “проиграла” в конкурентной “борьбе” с ней. Такая задача в Теории Эфира и не ставилась, так как она к науке не имеет отношения.
Могут быть и другие причины, например кому-то “наверху” показалось, что “такие” знания очень упростят людям понимание основ Мира и Природы, и значит, это будет шагом в сторону от Бога, а значит и уменьшит их власть. Но это лишь предположения, без цели найти причину среди массы возможных.
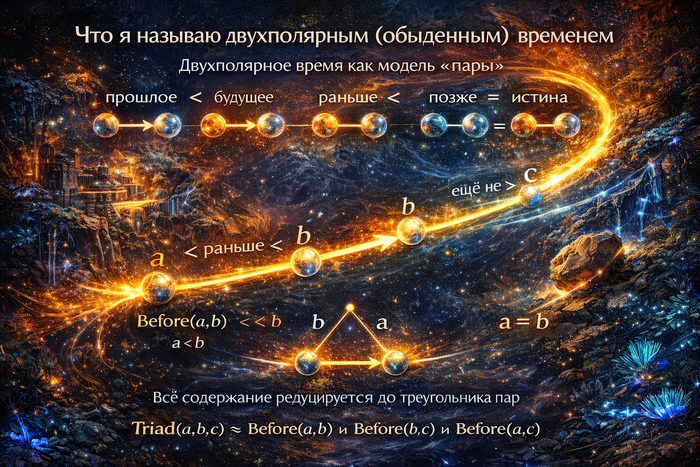
Двухполярная гравитация и время: максимально “на пальцах”, без заклинаний
Аннотация
Я описываю гравитацию в режиме L2 как вычислимый канал: источник -> потенциал -> ускорение. Время в L2 я трактую не как "вещественное начало” и не как “собственное время tau”, а как порядок фиксаций и внешний счёт в протоколе. Поэтому я запрещаю смешивать L2 с релятивистским языком (L3+), где фундаментальными становятся c и tau. Главная цель текста — дать минимальные тезисы, затем пошагово показать, что именно я считаю, что именно измеряю, где находится масштаб (kappa_B), и как устроена проверка против подмен понятий.
0. Теория в 2–3 тезисах
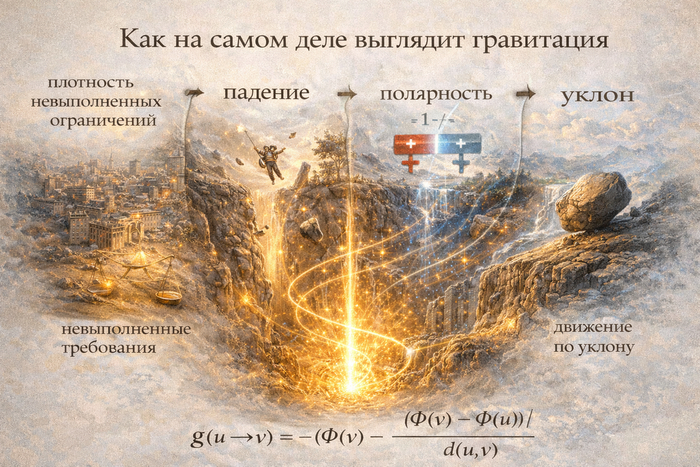
Гравитация (L2) — это не “сущность” и не “искривление времени”, а простое правило: если есть “карта высот” Phi, то тело ускоряется туда, где ниже. Формально:
a = -grad(Phi).Phi не берётся из поэзии. Она вычисляется из источника rho_g через оператор геометрии L:
L(Phi) = kappa * rho_g.
(На непрерывном носителе L похоже на лапласиан; на графе это дискретный оператор.)Время (L2) — это порядок фиксаций и внешний счёт шагов, а не “собственное время tau”. Поэтому внутри L2 нельзя легально выводить эффекты вида “tau зависит от v/c”: в L2 нет c и tau как фундаментальных объектов. Если они нужны — это другой режим (L3+), и переход должен быть явным.
Дальше я просто аккуратно раскрываю, что именно означают слова “источник”, “оператор”, “масштаб” и пр.
1. Почему я начинаю не с “пространства-времени”, а с определений
Слова вроде “пространство-время” часто используются как универсальный ответ. Проблема в том, что такие слова легко превращаются в заменитель определения. Я делаю наоборот: сначала фиксирую что измеряется, что вычисляется, что считается фундаментом, и что запрещено таскать внутрь режима.
Минимальный набор объектов L2:
Phi — потенциал (скалярная “карта высот”);
rho_g — источник (то, что “кормит” уравнение поля);
L — оператор геометрии (как именно “сравнивается” точка с окружением);
kappa — коэффициент масштаба (мост от формы уравнения к числам).
И минимальный результат, который должен получаться:
ускорение a определяется из Phi:
a = -grad(Phi)
(или графовый аналог по разностям Phi).
В этой конструкции нет “таинственных сущностей”. Есть функция, оператор и правило движения.
2. Полярность: с чего у меня начинается направление
Чтобы не подменять направление “интуицией автора”, я ввожу элементарный язык направления через сравнение.
Пусть есть шкала F(x) на состояниях x. Тогда полярность перехода:
pol(x -> y; F) = sign(F(y) - F(x)),
pol in {+1, -1}.
Это не украшение. Это минимальный способ сказать: “переход идёт вверх/вниз по выбранной шкале”. В L2 такая дисциплина важнее, чем кажется: если не фиксировать направление строго, затем легко продать любую интерпретацию как “следствие”.
3. Геометрия: где “поэзия” обычно прячется, и как я её выгоняю
3.1. Носитель может быть непрерывным или сетевым
Я допускаю два носителя:
континуум (классический случай);
граф G(V,E) с весами на ребрах.
Важна не философия носителя, а то, что оператор L должен быть задан явно.
3.2. Оператор L на графе (самый честный вариант)
На графе я записываю дискретный оператор так:
(L_phi)_i = sum_j w_ij * (phi_i - phi_j).
Смысл “на пальцах”: значение в узле сравнивается с соседями. Вес w_ij говорит, насколько сильна связь между i и j. Если веса выбирать, например, как ~ 1/d_ij^2, то оператор начинает вести себя метрически и напоминает непрерывную геометрию. Если выбрать иначе — это нужно обосновать.
Это место принципиально: на графе труднее “спрятать” допущение. Геометрия либо определена, либо её нет.
4. Ядро L2: что такое поле, и является ли оно вообще “полем”
Я употребляю слово “поле” в строгом, минимальном смысле.
Гравитационное поле в L2 — это не “вещество”, не “среда” и не “дух”. Это:
потенциал Phi как функция на носителе (континуум или граф);
правило, как из Phi получается ускорение.
Если нужно “на пальцах”: поле — это правило, которое каждой точке (или узлу) сопоставляет число Phi, а затем из разностей/градиента Phi даёт направление ускорения.
Формально:
L(Phi) = kappa * rho_g,
a = -grad(Phi).
4.1. Почему я не обязан считать поле “сущностью”
Потому что в минимальном инженерном смысле “поле” — это вычислимое распределение, которое позволяет делать предсказания. Если оно работает как вычислимый объект (и проходит проверки), мне не требуется добавлять “онтологию” сверх этого.
5. Где появляется “моя константа” и зачем она нужна
В L2 есть kappa — коэффициент, который задаёт масштаб связи между оператором, потенциалом и источником:
L(Phi) = kappa * rho_g.
Но пока kappa не согласован с единицами СИ, уравнение может быть красивым, но “немым” для лаборатории. Поэтому я ввожу режим B (СИ) и фиксирую калибровку масштаба.
В ньютоновском континуальном виде известна формула Пуассона:
Laplace(Phi) = 4piG*rho.
В режиме B я фиксирую мост:
kappa_B = 4piG
(при выбранной нормировке L и при beta = 1).
Здесь важна честная оговорка: kappa_B — не “новая константа природы”, а калибровка масштаба моего L2-уравнения в системе СИ. Иначе говоря, это печать “переведено в метры и секунды”.
6. Время в L2: что это такое “на пальцах”, и почему его нельзя смешивать с гравитационным полем
6.1. Определение времени L2
В L2 время — это порядок фиксаций (что раньше, что позже) и внешний счёт шагов протокола.
Я могу записать это так:
T2 = (E, <),
где E — множество событий/фиксаций, а < — отношение “раньше/позже”.
Числовая метка t в L2 — это удобный ярлык (номер записи, момент фиксации, шаг эксперимента). Но ядро времени здесь — порядок, а не “геометрия интервала”.
6.2. Почему нельзя смешивать поле и время
Потому что в L2 “поле” — это Phi и операторная связь L(Phi)=..., а “время” — это внешний параметр протокола и порядок фиксаций. Это разные типы объектов. Смешивание обычно выглядит так:
берут язык, где время является геометрической метрикой (это уже L3+);
затем незаметно втаскивают его в L2 и начинают делать выводы “как будто” это единый режим.
Я запрещаю такую контрабанду: если я говорю L2, я не имею права использовать фундаментальные объекты L3+.
6.3. Почему “парадокс близнецов” в L2 не формулируется
Потому что классическая формулировка опирается на:
c как фундаментальную константу;
tau как собственное время.
Типовая запись (упрощённо) выглядит как зависимость tau от v/c. Но в L2 нет c и tau как фундаментальных объектов. Следовательно, внутри L2 это не “опровергается” и не “подтверждается” — это не формулируется, потому что не принадлежит языку режима.
Если кому-то нужен разговор про tau и c — это допустимо, но это уже L3+, и переход должен быть объявлен явно.
7. Почему “простая проверка через земные средние величины” недостаточна
Часто предлагают проверку вида: “возьмём среднюю плотность Земли, радиус, g и покажем, что всё сходится”. Примерно так:
g = kappa_0 * rho_g * R_earth / 3,
kappa_0 = 4piG.
Я не отвергаю это как упражнение. Но я считаю его слабой проверкой, потому что оно почти замыкается само на себя. Главные проблемы:
Это круг по определению масштаба.
Если я уже принял G (или калибровку через G), то проверка через g и средние параметры Земли становится близкой к проверке алгебры, а не физики.Это не лабораторный тест.
Средние параметры Земли — агрегаты огромного числа допущений. Там трудно понять, что именно проверялось: модель поля, геометрия, конвенции или выбранный масштаб.Тест почти не может “провалиться” честно.
Если я свободно выбираю rho_g как “среднюю плотность”, беру R_earth и фиксирую kappa_B через G, то получить g порядка 10 м/с^2 — не удивительно. Это мало что говорит о корректности именно L2-структуры как проверяемой теории.
Поэтому такую проверку я оставляю как вводную иллюстрацию, но не выдаю её за серьёзную верификацию.
8. Минимальный набор действительно честных L2-проверок “прямо сейчас” (лабораторный уровень)
Здесь я формулирую проверки, которые:
не замыкаются на земные средние;
могут реально провалиться;
не требуют перехода в L3+.
8.1. Крутильные весы (тип Кавендиша): проверка канала “источник -> Phi -> a”
Суть: есть измеримая геометрия установки (расстояния), измеримые массы, измеримое угловое отклонение/период. Я строю предсказание ускорения или момента через Phi и сравниваю с измерением.
Логика L2 здесь проста:
я задаю источник rho_g так, чтобы он соответствовал физической плотности/массе в режиме B (beta=1);
считаю Phi (или эквивалентный момент/ускорение);
сравниваю с наблюдаемым отклонением.
Это тест, который может провалиться: если я неверно определил геометрию L, неверно задал веса w_ij, неверно нормировал оператор, я получу систематическое расхождение.
8.2. Проверка метрической нормировки оператора L на разных масштабах
Если я заявляю, что геометрия L метрически нормирована (например, веса ~ 1/d^2), то при изменении масштаба установки предсказания должны меняться определённым образом.
Простейшая идея: взять два расстояния d1 и d2 и проверить, что вклад связи масштабируется как (d2/d1)^2 (в той части, где это применимо). Это не “теория всего”, но это честная проверка того, что геометрия в модели действительно работает как заявлено.
8.3. Тест “без световых инвариантов”
Я формулирую утверждения так, чтобы в них не было скрытых ссылок на c и tau. Это не “анти-Эйнштейн”, это санитарная проверка режима. Если в выкладке неожиданно требуется c, значит я уже не в L2, и это должно быть признано явно.
9. Контрольные “заслоны” против подмен (то, что делает спор проверяемым)
Чтобы теория не превращалась в рассказ, я использую три контрольных барьера (внутри проекта они часто помечены как gate_*).
Контроль режима (gate_mode):
если утверждение помечено как L2/ModeB, запрещено использовать c и tau как фундаментальные объекты вывода.Контроль размерностей (gate_units):
если я пишу G, единицы обязаны быть m^3kg^-1s^-2;
если я пишу D = rho_earth/rho_water, это безразмерно.Контроль конвенций (gate_conventions):
нельзя молча менять g, R_earth, rho_water. Если меняю — фиксирую это явно и показываю, как сдвигается результат.
Эти барьеры превращают полемику в инженерную: спорят не “по вере”, а по месту, где нарушено правило.
10. Как должна выглядеть честная критика (и мой ответ на типовой комментарий)
Если мне говорят: “непонятно, слишком сложно”, я отвечаю так:
минимальные тезисы я уже дал (источник -> Phi -> ускорение; время как порядок фиксаций; запрет контрабанды c и tau в L2);
дальше я готов обсуждать строго: что именно непонятно — определение источника, оператор геометрии, масштаб kappa, или порядок времени.
Если мне говорят: “любая теория должна быть в двух тезисах”, я отвечаю спокойно:
в двух тезисах можно дать ядро; я это делаю;
но проверяемой теорией это становится только тогда, когда “два тезиса” превращаются в измеримые утверждения и проходят контроль размерностей и конвенций.
Заключение
Мой L2 — это не попытка “объяснить всё”. Это попытка сделать гравитацию минимальным, проверяемым модулем:
поле как потенциал Phi;
геометрия как оператор L;
источник rho_g;
масштаб как калибровка в СИ через kappa_B = 4piG;
время как порядок фиксаций, а не как собственное время tau.
И главное: я строю не только формулы, но и дисциплину, которая запрещает незаметные подмены. Именно это превращает разговор о гравитации и времени из литературного жанра в воспроизводимую процедуру.
Библиографические ориентиры (без ссылок)
Newton I. Philosophiae Naturalis Principia Mathematica. 1687.
Poisson S.-D. Memoire sur la theorie du magnetisme. 1824 (уравнение Пуассона в классической форме).
Cavendish H. Experiments to determine the Density of the Earth. Philosophical Transactions of the Royal Society of London. 1798.
CODATA Recommended Values of the Fundamental Physical Constants (актуальные выпуски, сводные значения G).
P.S. (для тех, кто пишет: "ничего не понятно, скажи в двух фразах")
Моя L2-гравитация устроена максимально просто: я задаю источник rho_g, считаю потенциал Phi из уравнения L(Phi) = kappa*rho_g, а ускорение получаю как a = -grad(Phi). Это "карта высот": куда ниже по Phi, туда и тянет. Никаких "сущностей" и "искривлений времени" на базовом уровне.
Время в L2 - не "вещь" и не "собственное время tau", а порядок фиксаций и внешний счет шагов протокола. Поэтому внутри L2 нельзя честно выводить формулы типа tau = ... (v/c): в L2 нет фундаментального c и нет tau. Если вы хотите c, свет и собственное время - это другой режим (L3+), и переход туда надо объявлять явно, а не протаскивать тайком.
Проверяемость: я не прошу "поверить". Я предлагаю спорить по процедуре: источник данных -> claim с условиями -> валидатор -> гейты (режим/единицы/конвенции) -> расчет -> отчет. Если вам кажется, что я ошибся, укажите не "ересь", а конкретно: какой гейт не пройден, где размерность сломана, где подменен режим или конвенция.
P.P.S. Почему "земная проверка через средние" (g, R_earth, средняя rho) не является серьезным тестом: она слишком легко замыкается на выбранный масштаб и почти не может честно провалиться. Честные L2-проверки начинаются там, где есть лабораторная установка (например, крутильные весы): измеримые массы/расстояния/период/отклонение, и расчет, который реально может не сойтись, если у вас неверно определены L, веса, нормировка или мост к СИ.
Вся матрица мышления и теория доступна в ChatGPT
Просто вставьте в новый чат архив
# Текст для вставки в новый чат: следуй инструкциям в файле
Как выглядит честная полемика с моей позиции
Если вы хотите спорить — спорьте. Но не как на Пикабу, а как в лаборатории.
Не “это похоже на ересь”, а:
какой claim неверен,
какой гейт не пройден,
где размерность нарушена,
какие конвенции подменены,
какой источник добавляет систематику.
Это и есть моя цель: сделать так, чтобы спор стал воспроизводимым. Просто обратитесь к ChatGPT.
Читайте также:
Минималистическая теория гравитации
О чистоте мышления в физике
В академической среде существует привычка произносить "пространство-время" как готовый ответ, почти как формулу-оберег. Я предпочитаю иной порядок рассуждения и спрашиваю вежливо, но настойчиво: если мы хотим оставаться в физике, а не в риторике, то начнем с определений, с оператора и с масштаба. Это не дерзость и не поза, а элементарная гигиена мышления.
Три допущения и три запрета
При построении теории я постоянно вижу два типовых соблазна.
Первый соблазн - "охватить всё сразу": смешать ньютоновскую механику, специальную теорию относительности, квантовую механику, идею эфира и несколько метафор об "энергии как сущности" в единый ковёр. Такой ковёр выглядит эффектно, пока не потребуется показать швы: где именно находятся определения, какие величины измеримы, какие операторы действуют и что является масштабом.
Второй соблазн - объявить минимализм, но тайно протащить внутрь теории то, от чего якобы отказались. Это и есть контрабанда понятий: когда фундаментальные объекты не вводятся явно, но начинают работать "между строк" и незаметно менять смысл уравнений.
Мой подход в режиме L2 устроен проще и, главное, честнее. Я оставляю три базовых элемента:
полярность как способ задать направление перехода;
геометрию как рабочий оператор на выбранном носителе;
поле как потенциал и правило движения.
И столь же строго исключаю из L2 три вещи:
световой инвариант c в статусе фундамента;
собственное время tau в статусе фундамента;
смешение подходов, когда к ньютоновской механике "подливают" элементы СТО и затем называют это "единым языком".
Если такая строгость кажется избыточной, то это означает лишь одно: давно не приходилось наблюдать, как корректная на вид теория разрушается из-за одной скрытой подмены терминов.
Полярность: предельно простое начало
Хорошая физика часто выглядит слишком трезво для тех, кто предпочитает таинственность. В моем случае трезвость начинается с того, что я не ввожу "великие сущности", а беру простое сравнение.
Я задаю шкалу F(x) на состояниях x и определяю полярность перехода так:
pol(x -> y; F) = sign(F(y) - F(x)), pol in {+1, -1}.
Здесь нет ничего, кроме знака разности. Но именно это и является дисциплиной: направление фиксируется формально, а не "по интуиции автора". Важное уточнение: полярность не является свойством тела; она относится к переходу x -> y относительно выбранной шкалы F. Это снимает множество псевдоонтологических соблазнов и заставляет говорить в языке проверяемых операций.
Геометрия: от гладкости к честной дискретности
Гладкие пространства удобны: они эстетичны и наследуют классической математической школе. Однако у них есть методологический риск: на гладком фоне легко спрятать неопределенность, замаскировать допущение под "естественность" и затем обсуждать уже не физику, а интерпретацию.
Поэтому я часто выбираю граф как носитель. На графе невозможно "сделать вид", что все определено само собой: приходится явно задать, что является соседством и каковы веса связи.
Тогда оператор поля становится прозрачным. В простейшем виде:
(L_phi)_i = sum_j w_ij * (phi_i - phi_j).
Если веса w_ij выбрать, например, пропорционально 1/d_ij^2, то оператор приобретает метрический характер и начинает напоминать континуальный лапласиан. Если веса выбираются иначе, это необходимо обосновать. Такой стиль исключает значительную часть псевдофизических построений, потому что заставляет автора отвечать на вопрос: "где именно у вас геометрия, а где - риторика?".
Ядро L2: поле и движение без лишних сущностей
Суть конструкции я записываю без украшений:
L(Phi) = kappa * rho_g, a = -grad(Phi).
Здесь:
Phi - потенциал;
rho_g - источник;
L - оператор геометрии;
kappa - коэффициент масштаба;
a - ускорение.
Принципиально важно то, чего здесь нет. Я не использую "силу как сущность" и не прибегаю к "туманным энергиям". Поле в L2 - это функция (потенциал), движение - это ориентация по градиенту (или дискретному аналогу). Это и есть минимализм, который сохраняет физический смысл и проверяемость.
"Моя константа": не открытие, а калибровка
Читатель часто ожидает увидеть "новую константу". Я предпочитаю говорить иначе: уравнение без масштаба может быть изящным, но без масштаба оно остается немым для измерений.
Гравитационная постоянная G - это параметр, который делает закон тяготения числовым законом в системе СИ. В этом смысле G - регулятор масштаба, а не персонаж метафизики.
В L2 у меня есть коэффициент kappa в уравнении поля. Чтобы L2 "говорил" на языке СИ, я фиксирую калибровку в режиме B:
kappa_B = 4piG.
Это не претензия на "открытие". Это печать согласования: выбран масштаб, задан мост к СИ, и после этого можно корректно сравнивать модель с лабораторными величинами.
Почему я не беру G из справочника как окончательную истину
Можно взять G из справочника и прекратить разговор. Но тогда теория превращается в проповедь: число дано "свыше", а проверяемость подменяется ссылкой на авторитет.
Я действую иначе: строю процедуру, которая сама показывает, откуда берутся числа и на каких условиях они допустимы. В виде дисциплинированной цепочки:
открытые источники (исторические и современные измерения, датасеты, протоколы установок);
извлечение наблюдений или параметров;
сбор утверждений (claims) вместе с условиями и конвенциями;
проверка валидатором;
прохождение гейтов;
формирование облака оценок;
выбор опорного значения G_anchor;
фиксация kappa_B на основе выбранного репера.
Так появляется не только число, но и контролируемая методология. А именно методология отделяет теорию от мнения.
Гейты: инструмент против самообмана
Слово "гейт" звучит технически, но по сути это формализованный здравый смысл. Я использую три базовых гейта.
Gate_mode: если утверждение маркировано как L2/ModeB, запрещено использовать c и tau как фундаментальные объекты вывода.
Gate_units: если утверждение относится к G, единицы обязаны быть m^3kg^-1s^-2; если утверждение относится к D = rho_earth/rho_water, оно обязано быть безразмерным.
Gate_conventions: нельзя молча менять g, R_earth, rho_water. Если параметры меняются, это оформляется явно, и показывается влияние на результат.
Эти три гейта отсеивают большую часть "логической жонглировки": не обязательно злонамеренной, но почти всегда разрушительной для воспроизводимости.
Время: дверь, которую я сознательно держу закрытой в L2
Обычно сразу звучит вопрос: "а как же относительность?". Я отвечаю спокойно: в L2 время - это внешний параметр счета и порядок фиксаций, но не геометрия интервала, не собственное время и не метрика Минковского.
Отсюда следует:
в L2 "парадокс близнецов" не формулируется, потому что нет tau и c в статусе фундаментальных объектов;
если требуется говорить о tau, необходимо перейти в L3+, честно назвать режим, построить мост и пройти гейты.
Иначе получается не физика, а контрабанда: смысл переносится "в кармане" вместе с чужой валютой, минуя таможню определения.
Как должна выглядеть честная полемика
Я не запрещаю спорить; напротив, я считаю спор необходимым. Но спор должен быть лабораторным по стилю, а не салонным.
Вместо "это похоже на ересь" следует говорить:
какое утверждение некорректно;
какой гейт не пройден;
где нарушена размерность;
где подменены конвенции;
какой источник дает систематическую ошибку.
Цель проста: сделать полемику воспроизводимой, а следовательно - физической.
Эпилог: где Эйнштейн остается уважаемым гостем
В моей конструкции Эйнштейн не является врагом. Он - уважаемый гость своего режима. В L2 я строю гравитацию из потенциала, оператора и источника; калибрую масштаб честно; отсеиваю подмены гейтами; трактую время как порядок и счет, а не как универсальную метрику.
Если спросить, зачем все это, ответ прост: чтобы теория была не рассказом, а воспроизводимой процедурой, которую можно проверять и критиковать без мистики и без заклинаний.
Вся матрица мышления и теория доступна в ChatGPT
Просто вставьте в новый чат архив
# Текст для вставки в новый чат: следуй инструкциям в файле
Как выглядит честная полемика с моей позиции
Если вы хотите спорить — спорьте. Но не как на Пикабу, а как в лаборатории.
Не “это похоже на ересь”, а:
какой claim неверен,
какой гейт не пройден,
где размерность нарушена,
какие конвенции подменены,
какой источник добавляет систематику.
Это и есть моя цель: сделать так, чтобы спор стал воспроизводимым. Просто обратитесь к ChatGPT.
Читайте также:
Как я получил собственную константу (каппа_B,anchor = 4 pi G_anchor = 8.274 *10^-10) и зачем она нужна
Глава 1. Корпус источников и извлечение исходных чисел «на пальцах»
0. Что я называю «собственной константой» в этой работе
Сразу фиксирую смысл, чтобы не было подмены. Моя «собственная константа» — это не “новая константа природы”, а проектный коэффициент моста между моей L2-формализацией (режим B, СИ) и числом G (гравитационная постоянная) в СИ.
Я обозначаю его так:
κ_B = 4 pi G (канонический мост режима B при β = 1),
а в практическом контуре, когда я строю «облако источников» и выбираю якорь, получается κ_B,anchor = 4 pi G_anchor.
Далее в этой главе я подробно показываю, по каким конкретным работам я делал расчёты и какие именно числа из них извлекал.
1) Источник №1: Кавендиш 1798 (первичка)
Библиографическая ссылка: Henry Cavendish. Experiments to Determine the Density of the Earth. 1798. Philosophical Transactions of the Royal Society of London (в PDF-репринте).
1.1. Что именно я беру из текста Кавендиша (самое важное)
У Кавендиша есть два уровня данных:
Сырые журнальные ряды: времена “mid. of vibration” (середины колебаний) по конкретным дням/режимам.
Сводная таблица результатов (в репринте это раздел “The following Table contains the Result of the Experiments”, внутренняя пагинация около стр. 520), где по каждому опыту уже выписаны: “Mot. arm” (смещение равновесия в делениях шкалы), “Time vib.” (период колебаний), “Density” (плотность Земли в долях плотности воды).
Для быстрого восстановления G в СИ мне достаточно колонки Density (потому что она уже “сжала” механику установки в один итоговый безразмерный результат D).
1.2. Число, которое я извлёк как «итог Кавендиша»
Кавендиш в “CONCLUSION” (в репринте это около стр. 521) фиксирует среднее:
D = 5.48 (плотность Земли в долях плотности воды).
Я дополнительно проверил воспроизводимость этого среднего по массиву значений из сводной таблицы. При отборе основного массива (23 значения, где период около 7 минут) получается:
D_mean ≈ 5.48348 (это практически совпадает с 5.48, написанным Кавендишем).
1.3. Мини-проверка «сырьё → период», чтобы было видно, что это не магия
Я взял один фрагмент журнальной страницы (где идут времена середин колебаний). Принцип простой:
беру последовательность отметок времени,
считаю разности соседних,
усредняю — получаю период одного колебания T.
На одном из фрагментов у меня получилось:
T ≈ 422.33 сек ≈ 7 мин 02 сек,
что согласуется с тем масштабом “Time vib.” около 7 минут в сводной таблице.
2) Источник №2: готовый открытый датасет по Кавендишу (29 опытов)
Библиографическая ссылка: Vincent Arel-Bundock (comp.). Cavendish (HistData): “Density of the Earth” dataset. (CSV-таблица 29 опытов;скачан файл формата Cavendish.csv).
2.1. Что именно я беру из CSV
Из CSV я беру столбец, соответствующий итоговым плотностям (в вашей работе использовалась финальная колонка серии “density3”, где значения заполнены).
Ключевая величина:
D_i = “плотность Земли в долях воды” по каждому опыту.
Дальше это становится прямым входом в пересчёт G.
2.2. Какой итог я получил по этому набору (в режиме B, СИ)
Я фиксирую канонические конвенции режима B (это именно проектный канон, а не “истина о воде при температуре X”):
g = 9.80665 м/с^2
R = 6 371 000 м
rho_water = 1000 кг/м^3
Тогда:
rho_earth = D * rho_water
G = 3 g / (4 pi R rho_earth)
В этой канонике удобно выделить коэффициент:
K = 3 g / (4 pi R rho_water)
тогда G = K / D
У меня в каноне получилось:
K = 3.674721761117883 × 10^-10
А по данным “density3” среднее:
D_mean ≈ 5.4835
Отсюда:
G_mean ≈ 6.7091570 × 10^-11 м^3 кг^-1 с^-2
sigma_G (разброс по серии) ≈ 2.3241 × 10^-12
Отдельно я делал “показательный” расчёт по одному опыту XIV (чтобы показать связку “сырые журналы → сводная формула → D”): там получилось
D ≈ 5.34
G ≈ 6.88 × 10^-11
Я подчёркиваю: это значение не “моя константа”, а демонстрация воспроизводимости вычисления на одном эксперименте.
3) Источник №3: Andrews & Bobowski (учебная репликация, 2018)
Библиографическая ссылка: T. Andrews, J. Bobowski. A Cavendish Experiment to Determine the Gravitational Constant. 2018. arXiv (препринт 1812.07644).
3.1. Что именно я беру из этой работы
Здесь мне важно не “их философское объяснение”, а то, что они дают полный протокол и параметры установки, по которым можно получить G в СИ.
В моём контуре это используется как независимая точка облака: другой автор, другой контур измерений, другой экспериментальный стиль.
3.2. Какой итог я зафиксировал у себя
По извлечённым параметрам и их неопределённостям я получил оценку:
G ≈ 6.49 × 10^-11 м^3 кг^-1 с^-2
sigma_G ≈ 0.49 × 10^-11 (то есть около 7.6% относительной неопределённости)
Важно: это не претензия на прецизионную метрологию, а честная учебная репликация, которая расширяет «облако» и проверяет устойчивость моста режима B на независимом материале.
4) Источник №4: UCSB (лабораторные данные по нескольким дням) + паспорт установки PASCO
Библиографические ссылки:
Advanced Laboratory (UCSB): Cavendish/Experiment1 dataset. (учебный набор данных; скачан репозиторий лабораторных работ).
PASCO Scientific. Cavendish Balance Setup / Lab Experiment. (паспорт/методичка установки; PDF).
4.1. Что именно я беру отсюда
Здесь я работаю уже не с “плотностью Земли”, а с типичным современным учебным контуром “крутильные весы”:
параметры геометрии (b, d, r и т. п.),
массы m и M,
период T (или omega = 2 pi / T),
оптический сдвиг ΔS и длина оптического плеча L,
перевод в угол: theta = ΔS / (2 L),
поправки (включая (1 − beta) в их обозначениях).
Ключевое: это даёт прямое вычисление G через баланс моментов крутильного маятника в их формуле, без “земной сферы”.
4.2. Какой итог я зафиксировал (3 дня как мини-облако)
По трём независимым дням у меня получились:
day1: G = 7.1247054 × 10^-11
day2: G = 6.0553407 × 10^-11
day3: G = 5.7754303 × 10^-11
Сводка как “облако по дням” (систематика именно через междневной разброс):
mean: 6.3184921 × 10^-11
sigma: 7.1209027 × 10^-12
Я специально держу эту группу как отдельный источник: она показывает, что даже при одном и том же контуре формул и одной установке междневная систематика может быть заметной — а значит, облако источников нужно не ради “красоты”, а ради честной диагностики.
5) Источник №5: Gundlach & Merkowitz (прецизионная лабораторная оценка, 2000)
Библиографическая ссылка: J. H. Gundlach, S. M. Merkowitz. Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Feedback. 2000. Physical Review Letters 85, 2869.
5.1. Что именно я беру
Здесь я беру заявленное авторами значение G и его 1σ-неопределённость как ещё одну независимую точку облака (другая методика, другой класс точности):
G = 6.674215 × 10^-11
σ = 0.000092 × 10^-11 (записано именно так; я сохраняю эту запись как заявленную авторами величину источника)
6) Что у меня получилось “на выходе” по источникам (без интерпретаций)
На уровне “какие цифры я реально получил из каких работ” итог этой главы такой:
Кавендиш (1798, D_mean ≈ 5.4835 в долях воды) → G_mean ≈ 6.7091570 × 10^-11, σ ≈ 2.3241 × 10^-12 (через канон g, R, rho_water).
Andrews–Bobowski (2018, учебная репликация) → G ≈ 6.49 × 10^-11, σ ≈ 0.49 × 10^-11.
UCSB (учебные данные, 3 дня) → G_day = {7.1247; 6.0553; 5.7754} × 10^-11, mean ≈ 6.3184921 × 10^-11, σ ≈ 7.1209 × 10^-12.
Gundlach–Merkowitz (PRL, 2000) → G = 6.674215 × 10^-11 с заявленной высокой точностью.
7) Зачем мне понадобился следующий шаг: перейти от “G из источников” к “моей константе κ_B,anchor”
Сами по себе числа G из разных работ — это просто набор оценок. Моя цель была другой: сделать из этого проектный мост, который нельзя подменить словами.
Поэтому я перешёл к якорной величине:
G_anchor = 6.584246365286102 × 10^-11
κ_B,anchor = 4 pi G_anchor = 8.274008004243246 × 10^-10
И сразу зафиксировал её статус: это не константа природы, а калибровка моста режима B, выведенная из моего облака источников по строгому контуру “данные → claims → валидатор → гейты → якорь”.
Глава 2. Мой расчётный контур: от статей к «облаку» и к якорю G_anchor → κ_B,anchor
0. Что я делаю в этой главе
В первой главе я перечислил, из каких работ я взял числа. Здесь я показываю ровно то, что обычно скрывают за словами “мы посчитали”: как именно я превратил набор статей/датасетов в одно воспроизводимое число.
Мой контур выглядит так:
данные источника → claim (что именно утверждается и в каких единицах) → валидатор (гейты) → “облако” оценок G → выбор якоря G_anchor → κ_B,anchor = 4 pi G_anchor.
1) Что такое claim и почему без него расчёт превращается в разговор
Для каждого источника я формирую не “цитату из PDF”, а claim — минимальный атом утверждения, который можно проверить.
В моём режиме B claim всегда содержит:
идентификатор источника (что это за работа/датасет),
тип источника (историческая плотность Земли D; прямое измерение G; учебная репликация; лабораторный дневник),
извлечённую величину (D или G) и её неопределённость,
единицы измерения и конвенции пересчёта (что именно я считаю “каноном” режима B),
способ получения числа (формула и список параметров, которые я подставляю),
“след” воспроизводимости: откуда взято значение (страница/раздел или колонка CSV, либо “итоговое значение авторов”).
Фокус здесь простой: я не спорю “чей текст красивее”, я фиксирую что именно было взято и как оно превращено в число.
2) Канон режима B в СИ, который я намеренно фиксирую
Чтобы у разных читателей не получались разные G “из-за воды при другой температуре” или из-за другого радиуса Земли, я ввожу канон режима B как проектное соглашение масштаба:
g = 9.80665 м/с^2
R = 6 371 000 м
rho_water = 1000 кг/м^3
Это не утверждение “о природе воды”, а определение калибровочной шкалы, в которой я строю мост из исторических и учебных данных в СИ.
Из этого канона получается удобная константа пересчёта:
K = 3 g / (4 pi R rho_water)
В моём контуре она вычисляется один раз и затем используется в формулах.
3) Как я считаю G из Кавендиша 1798, когда в источнике дана плотность Земли D
3.1. Что такое D в моём контуре
У Кавендиша (1798) и в датасете Cavendish.csv D — это безразмерная величина:
D = rho_earth / rho_water.
То есть это “плотность Земли в долях плотности воды”.
3.2. Как D превращается в G (мой шаг пересчёта)
Я использую стандартную ньютоновскую связь для однородной сферы:
g = (4/3) pi G R rho_earth.
Отсюда:
G = 3 g / (4 pi R rho_earth).
А так как rho_earth = D rho_water, то:
G = 3 g / (4 pi R D rho_water) = K / D.
То есть для Кавендиша в моём режиме B пересчёт предельно “на пальцах”:
беру D из источника,
делю K на D,
получаю G в СИ.
3.3. Какие числа реально получились в моём контуре
Для серии “density3” из Cavendish.csv я получил:
D_mean ≈ 5.4835
G_mean ≈ 6.7091570 × 10^-11 м^3 кг^-1 с^-2
sigma_G ≈ 2.3241 × 10^-12
Это и есть “источник Кавендиш” в моём облаке: не одна точка, а распределение по серии, сведённое к среднему и разбросу.
4) Как я считаю G из учебных репликаций и лабораторных данных, где G получают напрямую
Здесь я разделяю два случая.
4.1. Случай A: авторы дают параметры установки, а я воспроизвожу их формулу
Так устроен источник Andrews–Bobowski (2018): они дают уравнения, параметры и неопределённости. Я делаю следующее:
фиксирую их формулу получения G (в их обозначениях),
подставляю заявленные параметры,
если в источнике есть неопределённости, я считаю распределение G (например, Монте-Карло по их допускам),
свожу к среднему и sigma.
Результат, который я зафиксировал:
G ≈ 6.49 × 10^-11
sigma ≈ 0.49 × 10^-11
Смысл этой точки не в “точности”, а в независимости: другой экспериментальный стиль и другой набор систематик.
4.2. Случай B: лабораторный дневник по дням (UCSB), где систематика видна как междневной разброс
Для UCSB я не пытаюсь изображать “высокую метрологию”. Я честно считаю три независимых дня как три независимых оценки (одна и та же установка, но другой режим дрейфов, выравнивания, условий):
day1: 7.1247054 × 10^-11
day2: 6.0553407 × 10^-11
day3: 5.7754303 × 10^-11
Дальше я делаю то, что в таком материале честнее всего:
беру среднее по дням как точку источника,
беру sigma как междневной разброс (то есть систематика через повторяемость).
Получается:
G_mean(UCSB) ≈ 6.3184921 × 10^-11
sigma(UCSB) ≈ 7.1209027 × 10^-12
5) Как я учитываю прецизионную точку (Gundlach–Merkowitz, PRL 2000)
В работе Gundlach–Merkowitz (2000) я беру заявленное авторами значение и их 1σ-неопределённость как отдельный источник облака:
G = 6.674215 × 10^-11
σ = 0.000092 × 10^-11 (как заявлено в извлечении)
Важный принцип моего контура: я не позволяю прецизионной точке “поглотить” всё облако, если цель — калибровка моста по разнородным источникам. Иначе результат превращается в переименование одной лабораторной оценки.
Поэтому для выбора якоря я использую робастную процедуру, а не весовую “диктатуру” минимальной σ.
6) Как я строю «облако» и почему выбираю якорь через медиану средних
6.1. Что такое «облако» в моём смысле
Облако — это не свалка чисел, а набор нормализованных оценок одного и того же объекта:
каждая оценка приведена к СИ,
для каждой есть происхождение,
для каждой есть модель неопределённости (или честная систематика),
все оценки прошли валидатор.
Именно после этого я имею право обсуждать “якорь” и “смещение”, а не раньше.
6.2. Почему именно медиана средних по источникам
Источники в моём наборе гетерогенны:
исторический Кавендиш (через D и через канон g,R,rho_water),
учебные репликации с большой неопределённостью,
учебная серия по дням с сильной систематикой,
прецизионная лаборатория.
Если я просто сделаю взвешенное среднее по 1/σ^2, то один прецизионный источник почти полностью задавит остальные. Но мне на этом шаге нужен не “официальный G”, а устойчивый якорь калибровки, который отражает центр разнородного облака и не зависит от того, какой именно источник оказался самым “узким”.
Поэтому я делаю так:
для каждого источника беру его среднее значение G_source_mean,
сортирую источники по G_source_mean,
беру медиану этих средних,
если источников чётное число, медиана реализуется как среднее двух центральных значений.
Это робастный выбор: он устойчив к выбросам и не превращает “облако” в декорацию.
6.3. Какой якорь получился у меня
По моему контуру (после гейтов и сведения источников) я зафиксировал:
G_anchor = 6.584246365286102 × 10^-11 м^3 кг^-1 с^-2
И сразу перевёл его в мой проектный коэффициент моста:
κ_B,anchor = 4 pi G_anchor
κ_B,anchor = 8.274008004243246 × 10^-10 (в единицах СИ м^3 кг^-1 с^-2, как коэффициент масштаба в моём канале)
7) Что именно проверяет валидатор, чтобы это было не “число из текста”
Я считаю критически важным сказать это явно: моя “собственная константа” ценна не цифрой, а тем, что она получена контуром, который отсекает логические подмены.
В моём режиме B валидатор, как минимум, запрещает:
смешение L2 и L3 в одном вычислительном канале (никаких световых инвариантов внутри κ_B),
молчаливую смену канона (g, R, rho_water) без явного запроса изменения,
несогласованные размерности (G и κ_B должны иметь согласованные единицы),
“числа без происхождения” (нет claim → нет допуска в облако).
Именно это отличает κ_B,anchor от произвольной “авторской цифры”.
8) Зачем мне нужна κ_B,anchor практически
Я использую κ_B,anchor как технический мост:
в L2-уравнении поля вида L(Φ) = κ_B rho_g
κ_B задаёт масштаб перевода “внутреннего” расчёта в СИ при фиксированном режиме B.
Ещё раз: это калибровка моста, а не попытка заменить CODATA.
С этого момента я могу честно сказать: у меня не просто рассуждение о L2-гравитации, а воспроизводимая процедура, где любой читатель может взять те же открытые источники и получить те же числа при тех же конвенциях.
Глава 3. Что именно я утверждаю, зачем нужна κ_B,anchor и как читатель может всё перепроверить
0. Главное: что я НЕ утверждаю
Чтобы текст был честным, я начинаю с отрицаний — это защищает смысл результата.
Я не утверждаю, что “открыл новую физическую константу природы”.
Я не утверждаю, что получил значение G, которое надо противопоставить CODATA/NIST.
Я не утверждаю, что κ_B выводится из аксиом L2 как “неизбежная истина”.
Я утверждаю другое: я построил воспроизводимый мост из моей L2-формализации в СИ, и этот мост оформлен в виде проектной константы κ_B,anchor, полученной из открытых источников через протокол claims → валидатор → облако → якорь.
1) Что именно я утверждаю (в сильной, но корректной форме)
1.1. Утверждение A: у меня есть воспроизводимая процедура, а не “красивый текст”
Мой результат — это не число само по себе, а процедура, которая:
принимает открытый источник (PDF/CSV/лабораторные данные),
извлекает из него ровно определённую величину (D или G),
проверяет её гейтами (единицы, режим, конвенции),
приводит к общему формату,
строит облако оценок,
выбирает якорь.
Если процедуру повторить с теми же источниками и тем же каноном — получается тот же итог.
1.2. Утверждение B: κ_B,anchor — это проектная калибровка масштаба L2 в СИ
Я фиксирую мост режима B:
κ_B = 4 pi G (при каноне β = 1).
Далее я выбираю якорь G_anchor из облака источников и определяю:
κ_B,anchor = 4 pi G_anchor.
Именно κ_B,anchor является “моей” константой в узком проектном смысле: это число, которое закрепляет масштаб L2-канала в СИ в рамках выбранных конвенций и выбранной процедуры агрегирования.
2) Какие конкретные числа у меня получились в финале (и что они означают)
2.1. Канонические конвенции режима B (я их фиксирую как проектный закон)
g = 9.80665 м/с^2
R = 6 371 000 м
rho_water = 1000 кг/м^3
Это условия воспроизводимости пересчётов (особенно для пути через D).
2.2. Значение якоря и моей константы
По моему контуру “облака” я зафиксировал:
G_anchor = 6.584246365286102 × 10^-11 м^3 кг^-1 с^-2
κ_B,anchor = 8.274008004243246 × 10^-10 (в той же размерности, как коэффициент масштаба моста)
Смысл этих чисел:
G_anchor — “центр” моего текущего облака источников при выбранной робастной схеме якоря,
κ_B,anchor — соответствующий коэффициент моста для L2 уравнения LΦ = κ_B rho_g.
2.3. Что означает расхождение с опорным G_ref
Если сравнивать с рекомендованным G_ref (CODATA/NIST), то расхождение моего якоря порядка −1.349%.
Я трактую это не как “природа другая”, а как диагностический эффект моего текущего облака:
разные источники,
разные методики,
разные систематики,
плюс моя робастная схема якоря (которая не даёт одному прецизионному источнику полностью определять итог).
Для меня это показатель того, что процедура работает как инструмент диагностики и расширения облака, а не как “процесс объявления истины”.
3) Зачем мне вообще нужна κ_B,anchor в теории L2
3.1. Чтобы закрыть “дыру масштаба” между формализацией и СИ
В L2 у меня есть уравнение поля в форме:
L(Φ) = κ_B rho_g,
где rho_g в моей логике — не “килограммы”, а внутренний источник (плотность ограничений/связей/нарушений режима).
Без κ_B я могу рассуждать о форме уравнения, но не могу:
сравнивать с измерениями в СИ,
проверять численные масштабы,
проводить калибровку графовой геометрии на физическом материале.
κ_B,anchor закрывает эту дыру: это “цена перевода” моей формализации в СИ в режиме B.
3.2. Чтобы разделить “модель” и “метрологию” честно
Я считаю важным: κ_B не выдаётся как “аксиома природы”. Я показываю, из каких данных она получена и при каких соглашениях.
Это резко снижает риск псевдотеоретических заявлений: вместо “я вывел” я говорю “я откалибровал”.
3.3. Чтобы обеспечить возможность разговора с теорией через проверку, а не через веру
Когда κ_B,anchor встроена в граф и сопровождается гейтами, читатель получает способ взаимодействия:
спорить не о “правильности философии”,
а о том, прошёл ли claim валидатор,
какая конвенция взята,
как меняется якорь при расширении облака.
4) Как именно любой читатель может перепроверить мои расчёты (в практическом смысле)
Я специально оформил проект так, чтобы проверка не требовала “верить автору”.
4.1. Читатель берёт те же источники
Минимальный набор, чтобы повторить сюжет полностью:
Кавендиш 1798 (PDF репринт) — из него берётся D или даже воспроизводится D по одному опыту (как я делал для XIV).
Cavendish.csv — удобный способ быстро получить серию D_i и пересчитать G_i.
Andrews–Bobowski 2018 — независимая учебная репликация (G через их контур).
UCSB / PASCO — данные по дням с прямым вычислением G.
Gundlach–Merkowitz 2000 — прецизионная точка (G и σ) как внешний ориентир.
4.2. Читатель повторяет тот же канон режима B
Ключ к совпадению чисел: не менять канон (g, R, rho_water) молча.
4.3. Читатель повторяет ту же процедуру якоря
свести каждый источник к G_source_mean (и, где возможно, sigma),
взять медиану средних по источникам → получить G_anchor,
умножить на 4 pi → получить κ_B,anchor.
4.4. Читатель использует ИИ как “проверяющего”
Самый простой способ для человека, который не хочет вручную вычитывать формулы:
загрузить архив в новый чат,
следовать навигации,
попросить ИИ пройти по источникам, показать извлечённые числа, прогнать проверки и объяснить, где стоят гейты.
В результате читатель сможет не просто прочитать статью, а проверить, что именно в ней воспроизводимо.
5) Что нужно, чтобы перейти от калибровки к более сильным заявлениям (если это вообще нужно)
Если когда-либо я захочу заявлять не “у меня есть мост”, а “у меня есть устойчивое смещение” или “у меня есть новая поправка”, то минимальные условия такие:
Увеличить облако источников так, чтобы там были разные методики и независимые лаборатории в достаточном числе.
Ввести устойчивую статистику свода (робастность, веса, чувствительность к источникам).
Чётко отделить систематики источников от процедурной ошибки извлечения claims.
Сформулировать проверяемый тезис: “эффект сохраняется при расширении облака и при смене процедуры якорения”.
Пока это не сделано, я не называю результат “открытием”. Я называю его тем, чем он является: воспроизводимый мост L2→СИ, оформленный как κ_B,anchor.
6) Итог этой статьи в одной формуле
Я извлёк из открытых источников облако оценок G в СИ (режим B), выбрал робастный якорь и закрепил коэффициент моста:
G_anchor = 6.584246365286102 × 10^-11
κ_B,anchor = 4 pi G_anchor = 8.274008004243246 × 10^-10
Ценность результата — в протоколе, гейтах и воспроизводимости, а не в претензии на “новую физику”.
Если читатель сможет повторить те же шаги и получить те же числа, значит моя процедура работает. Если не сможет — значит ошибка локализуется, и я получаю конкретный объект для исправления, а не бесконечный спор о словах.
Вся матрица мышления и теория доступна в ChatGPT
Просто вставьте в новый чат архив
# Текст для вставки в новый чат: следуй инструкциям в файле
Как выглядит честная полемика с моей позиции
Если вы хотите спорить — спорьте. Но не как на Пикабу, а как в лаборатории.
Не “это похоже на ересь”, а:
какой claim неверен,
какой гейт не пройден,
где размерность нарушена,
какие конвенции подменены,
какой источник добавляет систематику.
Это и есть моя цель: сделать так, чтобы спор стал воспроизводимым. Просто обратитесь к ChatGPT.
Читайте также:
Трёхполярное пространство в L3-логике: почему мы живем в двухполярной «плоскости»
1) Что я называю трёхполярным пространством
Я называю трёхполярным пространством такое пространство, где первичным носителем смысла и структуры является не бинарная связь вида A—B, а триадное замыкание:
Close(A, B, C) = ☼.
Для меня ☼ — не “четвёртая сущность” и не число. Это маркер факта замыкания: триада допустима, непротиворечива и удерживается как единый акт в конкретной локе ℓ, то есть при конкретном множестве допустимых триад E_ℓ.
Отсюда следует мой принцип: если я описываю мир так, будто любые связи разлагаются на пары, то я заранее делаю проекцию трёхполярного на двухполярное. А значит, я заранее теряю ту часть реальности, где смысл возникает только в тройке.
2) Почему мой привычный мир кажется двухполярным («плоским»)
Я живу в мире бинарных проекций. Это “плоскость” не в геометрическом, а в режимном смысле: почти всё, что я измеряю, обсуждаю и кодирую, сводится к парам.
Я вижу три причины.
Первая причина: мои каналы наблюдения и описания устроены парно. Язык, классическая логика, привычный граф, цифровая техника, бытовое мышление — всё это фиксирует отношения вида “между двумя есть связь”.
Вторая причина: пары легче стабилизировать, чем триады. Двухполярные отношения проще сделать шумоустойчивыми и проверяемыми. Триада требует, чтобы третий полюс оставался структурно обязательным, а в моей повседневной практике “третье” обычно уходит в фон или в “контекст”, который не получает статуса полноценного элемента структуры.
Третья причина: двухполярность удобна доминанте. Двухполярный ум стремится к финальному ответу, победителю и единственной линии. Трёхполярная дисциплина требует альтернатив, контроля порядка и признания ветвлений. Это дороже. Поэтому моя культура и мои инструменты естественно тяготеют к плоскости.
3) Я фиксирую ещё один слой: трёхполярный мир имеет собственную «гравитацию»
Я ввожу для себя важное уточнение: у трёхполярного мира есть собственная гравитация, если трактовать гравитацию не как физическое поле в классическом смысле, а как меру притяжения к двухполярной плотности.
Я задаю это так.
Я считаю “массу” в двухполярной проекции как наибольшую плотность двухполярных связей на единицу пространства. Там, где связь A—B доминирует и заполняет пространство множеством устойчивых пар, моя картина мира становится “тяжёлой”: проекция уплотняется, всё начинает выглядеть как предметы, линии причинности и однозначные траектории.
Тогда “гравитация” в моей L3-интуиции — это степень, с которой трёхполярные структуры падают в двухполярные тени: чем больше плотность устойчивых пар на единицу пространства, тем сильнее тянет к плоскости, тем легче триады распадаются на пары и начинают выглядеть как обычные объекты.
В этом смысле я говорю: двухполярность создаёт собственный режим притяжения. Она формирует “массу” как максимальную плотность парных связей, и эта масса делает мир визуально и когнитивно плоским.
4) Как я определяю «трёхполярный объект» строго
Я называю объект трёхполярным не потому, что у него “три стороны”, а потому, что он определён только в триаде. Он не существует как самосущность. Он существует как роль взаимной определимости:
A = B * C,
B = A * C,
C = A * B,
и совместно: Close(A, B, C) = ☼.
Это для меня главный критерий: если я могу без потери смысла заменить триадную структуру набором парных рёбер (A—B, B—C, C—A), значит, передо мной не трёхполярный объект, а двухполярный объект с декорацией.
5) Почему трёхполярное пространство имеет радикально другие свойства
Я утверждаю, что трёхполярное пространство обладает свойствами, которые в двухполярной геометрии выглядят как парадокс.
5.1. Один объект может существовать как два или как три
В двухполярной “плоскости” я привык: объект либо один, либо два, и это счёт объектов одного типа.
В трёхполярном пространстве я мыслю иначе: “один объект” — это не количество экземпляров, а устойчивая конфигурация замыкания. Один и тот же исходный носитель может иметь разные устойчивые представления:
как “два” в виде двух устойчивых бинарных теней (двух проекций),
как “три” в виде сомкнутой триады, где три роли удерживаются как единый акт.
Я считаю нормальным, что объект в сомкнутом состоянии проявляется как три, а в проекции может выглядеть как два. Это не нарушение логики, это разные уровни описания: триадный носитель и бинарная тень.
5.2. Вырождается понятие прямой: она может быть одновременно и прямой, и кривой
Я фиксирую, что “прямая” — это понятие двухполярной геометрии: кратчайший путь между двумя точками в метрике, заданной на парах.
Но в трёхполярном пространстве первична не пара, а триада. Тогда траектория рассуждения, движения или изменения — это не “линия по парам”, а след по гиперрёбрам: цепочка триадных актов.
В такой геометрии то, что я в бинарной проекции считаю прямой, может соответствовать кривой в триадной структуре, и наоборот. “Прямая” перестаёт быть абсолютным объектом. Она становится свойством выбранной проекции и выбранной локи. Поэтому я говорю: в трёхполярном пространстве понятие прямой вырождается; оно может одновременно выглядеть прямым в одной тени и кривым в другой, потому что метрика и связность задаются не парами.
6) Мой спойлер про «невидимую точку»: почему сомкнутая триада может быть ненаблюдаемой
Я сознательно удерживаю тезис: сомкнутое трёхполярное образование может быть “невидимой точкой” для двухполярного наблюдателя.
В L3-терминах сомкнутость означает стабилизацию: если я взял некоторый набор S*, то дальнейшее замыкание в локе ℓ ничего не добавляет:
Cl_ℓ(S*) = S*.
Если триада замкнута и не даёт устойчивой бинарной тени (то есть не порождает таких A—B, которые сами по себе воспроизводимы как “объект”), то в двухполярном мире она проявляется как точка без тени — то есть практически как “ничто”.
Я не считаю это мистикой. Я считаю это свойством проекции: бинарный канал не способен увидеть то, что существует только как триадный акт.
7) Что для меня значит «разомкнутое» состояние и как оно становится видимым
Я различаю два типа разомкнутости.
7.1. Разомкнутость как ветвление оператора третьего
Если для пары (A, B) существует не один третий, а несколько:
Comp_ℓ(A, B) = {C1, C2, …}, и |Comp_ℓ(A, B)| > 1,
то у меня возникает структурная многополярность. Для плоского наблюдателя это выглядит как “аномалия”: одна и та же пара ведёт себя по-разному. Для меня это нормальное ветвление триадного мира, просто видимое в двухполярной тени.
7.2. Разомкнутость как сцепка с внешним контуром
Второй тип разомкнутости появляется, когда триадная связка начинает сцепляться с внешним контуром W (наблюдатель, мир, контекст). Тогда триада начинает порождать устойчивую бинарную тень: объект становится видимым как “вещь”, “событие” или “ограничение” в плоскости.
8) Я моделирую: как выглядят «реально трёхполярные объекты» в двух режимах
Я задаю минимальную модель.
Есть множество символов V.
Есть лока ℓ, то есть E_ℓ — допустимые триады.
Есть оператор Comp_ℓ(x, y) — множество третьих для пары.
Есть замыкание Cl_ℓ(S) — итеративное достраивание по Comp_ℓ.
8.1. Сомкнутый объект
Сомкнутый объект для меня — это минимально устойчивая триада {A, B, C}, где C однозначно восстанавливается из A и B, и после этого структура стабилизируется. В идеале такая триада не имеет самостоятельной бинарной тени. Тогда в плоскости она выглядит как “невидимая точка”.
8.2. Разомкнутый объект
Разомкнутый объект проявляется тремя способами.
Первый: как “мерцание” — одна и та же бинарная пара порождает разные исходы из-за ветвления Comp_ℓ.
Второй: как “объект-событие” — видимым становится сам акт достраивания третьего.
Третий: как “объект-ограничение” — пара наблюдается, но её поведение подчиняется закону, который нельзя вывести из пары без триадного носителя.
9) Итог: что я считаю главным
Я утверждаю четыре вещи.
Я живу в двухполярной “плоскости”, потому что мои каналы и культура фиксируют пары, а не триады.
Трёхполярный мир имеет собственную “гравитацию” к плоскости: чем выше плотность двухполярных связей на единицу пространства, тем сильнее триадная структура падает в бинарные тени и тем “тяжелее” выглядит мир.
Трёхполярное пространство обладает иными свойствами: один объект может проявляться как два или как три в сомкнутом состоянии; прямое может выглядеть кривым и наоборот, потому что первична триадная связность, а не парная метрика.
Реально трёхполярные объекты в сомкнутом состоянии могут быть “невидимыми точками”, а в разомкнутом — становятся видимыми как мерцание, как событие замыкания или как невидимое ограничение, управляющее поведением наблюдаемых пар.
Если я хочу сделать следующий шаг, я должен построить маленький демонстрационный мир: задать V, две локи E_ℓ1 и E_ℓ2, и показать на одном S0 два устойчивых замыкания, а затем посчитать “двухполярную массу” как плотность парных теней и показать, как меняется “гравитация плоскости”.
Продолжение: я строю демонстрационный «мини-мир» L3 и показываю две устойчивые реальности из одного старта
Теперь я задаю маленькое пространство символов, фиксирую две локи (два закона допустимости триад), получаю два устойчивых замыкания из одного и того же исходного материала, а затем считаю «двухполярную массу» и тем самым определяю, где и почему возникает “гравитация плоскости”.
10) Мини-мир: V, триады и простое правило замыкания
Я беру конечное множество символов
V = {A, B, C, D, E, G}.
Я задаю локу ℓ через множество допустимых триад E_ℓ. Триада — это гиперребро {x, y, z}, которое я читаю так:
Close(x, y, z) = ☼.
Дальше я фиксирую два оператора.
Оператор третьего:
Comp_ℓ(x, y) = { z ∈ V | {x, y, z} ∈ E_ℓ }.
Оператор замыкания множества S:
Cl_ℓ(S) строится итеративно: если x ∈ S и y ∈ S, и Comp_ℓ(x, y) содержит элементы, я добавляю их в S; повторяю, пока S перестаёт расти.
Это и есть мой минимальный “двигатель трёхполярной геометрии”: вывод и “геометрия” совпадают, потому что пространство задано не координатами, а замыканием по триадам.
11) Две локи: два закона допустимости для одного и того же V
11.1. Лока ℓ₁: «триадное разворачивание»
Я задаю E_ℓ1 так:
{A, B, C}
{A, C, E}
{B, C, E}
{C, E, G}
Интуитивно я делаю локу, в которой пара A,B неизбежно “втягивает” третий полюс C, затем порождается E, затем G.
11.2. Лока ℓ₂: «плоская стабилизация»
Я задаю E_ℓ2 так:
{A, B, D}
Я делаю локу, где та же пара A,B закрывается быстро и не “разворачивает” дополнительную сеть.
12) Один старт — два устойчивых мира: два замыкания
Я фиксирую один и тот же исходный материал:
S0 = {A, B}.
12.1. Замыкание в ℓ₁
Из S0 в ℓ₁ я получаю:
Comp_ℓ1(A, B) = {C}, значит S становится {A, B, C}.
Далее Comp_ℓ1(A, C) содержит E, и Comp_ℓ1(B, C) тоже содержит E, значит S становится {A, B, C, E}.
Далее Comp_ℓ1(C, E) содержит G, значит S становится {A, B, C, E, G}.
Дальше новых элементов не появляется.
Я фиксирую устойчивое замыкание:
S1* = Cl_ℓ1(S0) = {A, B, C, E, G}.
12.2. Замыкание в ℓ₂
В ℓ₂:
Comp_ℓ2(A, B) = {D}, значит S становится {A, B, D}.
Других триад нет, рост прекращается.
Я фиксирую второе устойчивое замыкание:
S2* = Cl_ℓ2(S0) = {A, B, D}.
Здесь для меня принципиально: я не меняю исходный материал S0. Я меняю только локу, то есть множество допустимых триад E_ℓ. Это и есть “два устойчивых мира одной и той же сцены” в строгом L3-смысле.
13) Я ввожу «двухполярную массу» и гравитацию плоскости
Теперь я формализую ваш тезис про гравитацию и делаю его частью модели.
13.1. Бинарная тень
Я определяю бинарную тень триады {x, y, z} как три парных связи:
(x—y), (y—z), (x—z).
Для замыкания S* я беру все триады, которые реально участвовали в достраивании, и объединяю их бинарные тени. Получаю множество парных связей E_shadow(S*).
13.2. Масса как плотность двухполярных связей
Я задаю “массу” как плотность двухполярных связей на единицу пространства. В мини-мире я беру “единицу пространства” как число вершин в замыкании:
Mass(S*) = |E_shadow(S*)| / |S*|.
Это ровно то, что я хотел зафиксировать: масса растёт, когда в данном объёме пространства накапливается много устойчивых бинарных связей.
13.3. Гравитация как притяжение к плоскости
Я трактую “гравитацию плоскости” как степень приближения структуры к двухполярности через рост этой массы:
g(S*) = Mass(S*).
Это не физическое утверждение о гравитации как о поле в общей теории относительности. Это режимная модель: где больше плотность парных связей, там сильнее “притяжение к плоскости”, то есть сильнее тенденция видеть и фиксировать мир в бинарных объектах.
14) Я считаю массу для двух миров и показываю, где сильнее «притяжение к плоскости»
14.1. Масса мира ℓ₁
В ℓ₁ участвовали триады:
{A,B,C}, {A,C,E}, {B,C,E}, {C,E,G}.
Их бинарная тень даёт пары:
A—B, A—C, B—C, A—E, C—E, B—E, C—G, E—G.
То есть |E_shadow(S1*)| = 8, а |S1*| = 5.
Mass(S1*) = 8/5 = 1.6.
14.2. Масса мира ℓ₂
В ℓ₂ участвовала одна триада {A,B,D}, её тень:
A—B, A—D, B—D.
То есть |E_shadow(S2*)| = 3, а |S2*| = 3.
Mass(S2*) = 3/3 = 1.0.
14.3. Интерпретация
Я получаю строгий результат на игрушечной модели: в локе ℓ₁ масса больше, чем в локе ℓ₂. Это означает, что ℓ₁ создаёт более “тяжёлую” бинарную проекцию, то есть более сильную гравитацию плоскости. Там, где триадный мир разворачивает сеть, он одновременно порождает больше парных теней на единицу объёма, и наблюдатель легче перепутает триадную природу объекта с “вещью плоского мира”.
И наоборот, ℓ₂ даёт мало структуры, но тень получается максимально “чистая” и однозначная: три вершины и три парных связи. Это плоскость, которая быстро стабилизируется и не раскрывает триадную глубину.
15) Я показываю, как в трёхполярном пространстве вырождается «прямая» и почему один объект может быть «двумя» или «тремя»
15.1. Объект как два или как три
Я считаю трёхполярный объект не “вещью”, а устойчивой конфигурацией замыкания. Тогда один и тот же объект O в триадном носителе может проявляться двумя способами.
В сомкнутом состоянии я вижу триаду как атом: {A,B,C}. Для меня это один объект-актом связи, и он “существует как три” по ролям участия.
В двухполярной тени та же структура легко редуцируется до пары A—B как “главного ребра”, а C уходит в скрытый полюс. Тогда для наблюдателя объект “существует как два” в виде устойчивой пары, хотя на уровне носителя он триаден.
Я считаю это нормой трёхполярного пространства: счёт “сколько объектов” становится зависимым от локи и от проекции, потому что объект — это не экземпляр, а замыкание.
15.2. Почему прямая вырождается и может быть одновременно прямой и кривой
В двухполярной геометрии “прямая” основана на парной метрике: кратчайшее между двумя точками.
В трёхполярной геометрии первична не пара, а триада. Траектория становится “следом по гиперрёбрам”, то есть цепочкой триадных актов. Тогда один и тот же след, будучи спроецирован на бинарную тень, может выглядеть как прямая в одной локе и как кривая в другой, потому что меняется закон допустимости E_ℓ и меняется сам тип минимальности. Прямая перестаёт быть абсолютным объектом и превращается в эффект выбранной проекции.
16) Я добавляю финальный штрих: как получить «две устойчивые реальности» внутри одной локи и зафиксировать DIV и κ
Если я расширю одну локу так, чтобы пара (A,B) допускала два разных третьих полюса, я получу ветвление:
Comp_ℓ(A, B) = {C, D}.
Тогда из одного S0 = {A,B} я получаю два разных устойчивых замыкания в рамках одной и той же локи, а не только при смене локи. В этом месте я естественно измеряю структурную многополярность как число различимых устойчивых замыканий, достижимых из S0. Это и есть DIV в чистом виде.
А κ я фиксирую как чувствительность к порядку и выбору ветвей: разные порядки и выборы третьего могут давать разные S*. В трёхполярном пространстве это не “ошибка”, а диагностический факт: порядок и ветвление являются частью геометрии.
Итоги
Я построил минимальный L3-мир, где один старт S0 даёт два устойчивых мира через смену локи. Я ввёл массу как плотность двухполярных связей на единицу пространства и показал, что “гравитация плоскости” усиливается там, где бинарная тень становится плотнее. Я также зафиксировал, что в трёхполярном пространстве объект может проявляться как “два” или как “три”, а понятие прямой вырождается и становится проекционным эффектом.
Как я переношу бинарный графовый слой в 3-однородный гиперграф, не ломая обратную совместимость
Я перехожу от философского описания к инженерной дисциплине. Мне нужно сделать миграцию так, чтобы трёхполярный носитель стал первичным, но старый бинарный слой продолжал работать как проекция и как интерфейс для внешних потребителей. Это означает: я мигрирую не “картинку”, а контракт допуска, где у каждого шага есть гейты, отчёты и критерии завершения.
1) Что именно я переношу: не рёбра, а смысловые атомы
Я фиксирую исходную ситуацию.
Бинарный слой задаётся как G₂ = (V, E₂), где E₂ — множество парных рёбер.
Трёхполярный слой задаётся как H₃ = (V, E₃), где E₃ — множество гиперрёбер-триад {x, y, z}.
Ключевой тезис: я не могу “просто взять треугольники” и назвать их триадами. Триада в L3 — это не факт взаимной связности, а факт взаимной определимости и замыкания. Поэтому миграция обязана включать правило, по которому триада считается допустимой в локе ℓ.
2) Мой принцип обратной совместимости: бинарный слой становится тенью, но не исчезает
Я сохраняю бинарный слой как стабильный интерфейс, но меняю его статус.
Я считаю, что:
E₂ больше не является первичной онтологией, а является проекцией E₃.
Я фиксирую проекцию явно:
Shadow(E₃) = множество пар (u, v), которые являются тенью гиперрёбер, то есть для каждого {x, y, z} ∈ E₃ я добавляю пары (x, y), (x, z), (y, z).
Дальше я принимаю контракт:
Любая внешняя система, которая “понимает только пары”, работает по Shadow(E₃).
Таким образом, я не ломаю прошлые запросы “соседство”, “путь”, “компонента связности”. Я позволяю им работать на тени, а не на первичном смысле.
3) Как я строю триады E₃ из бинарного слоя E₂: три правила, три разных класса триад
Я отделяю три класса триад, потому что у них разная степень обоснованности.
3.1. Триады-следствия из явного L3-контракта
Это идеальный случай: триада появляется, потому что она прямо задана моими артефактами и протоколами L3, а не добыта эвристикой. Такая триада сразу относится к локе ℓ и имеет смысловое описание, что именно замыкается.
Эти триады я считаю “жёсткими”.
3.2. Триады-миграции из структурных мотивов
Если у меня в бинарном графе встречается устойчивый мотив из трёх узлов, я не объявляю его триадой автоматически. Я использую мотив лишь как кандидат.
Кандидат в триаду проходит проверку “оператора третьего”: должна существовать интерпретация, при которой двое восстанавливают третьего в данной локе.
Если такой интерпретации нет, мотив остаётся просто треугольником тени.
3.3. Триады, порождённые замыканием Cl_ℓ
Если у меня есть начальные множества S₀ и правила Comp_ℓ, я могу порождать триады как факты замыкания в локе. В этом случае триады являются продуктом машины вывода и имеют наибольшую ценность для L3, потому что они не описательные, а операциональные.
4) Как я фиксирую локи: лока не красит узлы, она выбирает E_ℓ
Я удерживаю базовую дисциплину: полярность не принадлежит узлу. Значит, лока не может менять “цвет вершины”.
Я задаю локу ℓ только как выбор допустимых триад:
E_ℓ ⊆ { {x, y, z} | x, y, z ∈ V }.
Тогда H_ℓ = (V, E_ℓ).
В миграции это важно: я переношу не один гиперграф, а семейство гиперграфов по локам. Это и позволяет мне объяснять “две устойчивые реальности одной сцены” как разные E_ℓ при одном V.
5) Контракт миграции: какие операции Ω_min я разрешаю, чтобы не разрушить смысл
Я задаю минимальные операции миграции так, чтобы нельзя было “нарисовать красивую структуру” и тем самым узурпировать смысл.
Я использую следующий набор Ω_min для миграции.
Добавление триады-кандидата с обязательной аннотацией локи ℓ и основанием появления.
Перевод триады-кандидата в триаду-допускаемую только после прохождения гейтов.
Добавление правила Comp_ℓ(x, y) только при фиксированном перечне источников и при контроле обратной совместимости.
Запрет удаления: ни E₂, ни E₃ не уменьшаются. Любое уточнение делается добавлением нового статуса или нового слоя локи, а не стиранием старого.
6) Гейты миграции: когда я считаю шаг корректным, а когда дефектным
Я ввожу набор гейтов, которые каждый релиз миграции обязан пройти.
6.1. Гейт целостности
Каждое добавленное гиперребро {x, y, z} обязано ссылаться на существующие x, y, z ∈ V.
Каждая триада обязана иметь привязку к локе ℓ.
6.2. Гейт смысловой согласованности
Для каждой триады я фиксирую её смысл как факт замыкания: что именно считается “☼” в данном контексте. Если триада не имеет смыслового описания, она может существовать только как кандидат, но не как допустимая.
6.3. Гейт обратной совместимости
Я проверяю, что базовые бинарные запросы дают прежние результаты в допустимых пределах.
Я формулирую это так: для множества контрольных запросов Q₂ результаты на старом графе должны совпадать с результатами на тени нового гиперграфа.
Там, где совпадение невозможно по природе модели, я обязан зафиксировать явные правила расхождения и добавить это в контракт версии, иначе миграция считается дефектной.
6.4. Гейт κ: контроль чувствительности к порядку
Я провожу замыкание одним и тем же S₀ разными порядками применения Comp_ℓ и сравниваю устойчивые результаты.
Если κ резко растёт после миграционного шага, я обязан классифицировать это как одно из двух.
Это нормальное выявление скрытой многополярности, тогда я обязан добавить “другое” как независимый контур и усилить π_K.
Это дефект миграции, если рост κ объясняется добавлением сомнительных триад без смысла и без привязки к локе.
6.5. Гейт DIV: пороги структурной многополярности
Я считаю структурную многополярность не по количеству формулировок, а по числу различимых устойчивых замыканий из заданных S₀ в заданных локах.
Я ввожу порог DIV_min для демо-сценариев: если модель претендует на многополярность, она обязана показать не менее двух независимых устойчивых замыканий в контролируемой задаче, и эти замыкания не должны сводиться друг к другу без разрушения инвариантов.
6.6. Гейт инвариантов I
Любая миграция считается дефектной, если новые триады или новые правила Comp_ℓ приводят к замыканиям, нарушающим I_logical, I_ethical, I_safety или I_context.
Это гейт “против красивого замыкания любой ценой”.
7) Критерии завершения миграции: когда я считаю переход законченным
Я считаю миграцию завершённой не тогда, когда “всё стало гиперграфом”, а тогда, когда выполнены три условия контракта.
7.1. Покрытие первичных артефактов
Каждый артефакт, который в проекте считается L3-значимым, имеет представление в E₃ в виде допустимых триад в соответствующих локах.
7.2. Эквивалентность тени по ключевым бинарным интерфейсам
Для контрольного набора запросов бинарного уровня результаты на старом слое и на тени совпадают в пределах заранее указанной нормы. Это означает, что внешние интеграции не ломаются.
7.3. Наличие воспроизводимых демо-замыканий
Я обязан иметь хотя бы один публично воспроизводимый сценарий, где из одного S₀ получаются два устойчивых замыкания в разных локах, и я показываю κ и DIV как измеряемые параметры, а не как лозунг.
Только после этого я имею право говорить, что трёхполярный слой стал первичным, а бинарный слой окончательно закреплён как интерфейсная тень.
8) Как я организую CI-контур и «заморозку интерфейсов»
Чтобы миграция не превращалась в ручное творчество, я ввожу дисциплину релизов.
Я версионирую контракт L3: что считается входами, выходами, допустимыми Ω_min и гейтами.
Я замораживаю внешний бинарный интерфейс: любые изменения видимых бинарных результатов требуют отдельного решения на уровне π_G, а не “исправления” внутри кейса.
Я автоматизирую гейты: отчёт по целостности, отчёт по обратной совместимости, отчёт по κ и DIV, отчёт по инвариантам.
Это и есть моя “режимная дисциплина” на практике: границы преобразований задаются не настроением автора, а контрактом допуска.
Итог
Я описал, как я делаю миграцию из бинарного графа в 3-однородный гиперграф так, чтобы трёхполярный слой стал первичным, но бинарная плоскость сохранилась как интерфейсная тень. Я зафиксировал Ω_min миграции, набор гейтов, критерии завершения и роль CI-контуров и π_G в заморозке “верха”.
Вся матрица мышления и теория доступна в ChatGPT
Просто вставьте в новый чат архив
# Текст для вставки в новый чат: следуй инструкциям в файле
Как выглядит честная полемика с моей позиции
Если вы хотите спорить — спорьте. Но не как на Пикабу, а как в лаборатории.
Не “это похоже на ересь”, а:
какой claim неверен,
какой гейт не пройден,
где размерность нарушена,
какие конвенции подменены,
какой источник добавляет систематику.
Это и есть моя цель: сделать так, чтобы спор стал воспроизводимым. Просто обратитесь к ChatGPT.
Читайте также:
UPD:
Смысл в том, что мы живём в двухполярном мире не потому, что сама реальность “двухмерна”, а потому, что наши каналы восприятия и инструменты описания сводят трёхполярную структуру бытия к парным проекциям.
Когда человек говорит: “я могу двигаться в трёх измерениях, я вращаюсь вокруг Солнца, лечу с Галактикой и т.д.” — он прав в физическом смысле координат и скоростей. Но текст про трёхполярность говорит не о геометрической размерности, а о типе структурного восприятия. “Полярность” — не направление в пространстве, а логическая связность, способ удерживать смысл между элементами.
Почему наш мир кажется двухполярным
Наши языки и логика устроены парно.
Всё, чем мы оперируем — “истина/ложь”, “да/нет”, “свет/тьма”, “плюс/минус”. Даже граф, на котором строится рассуждение, соединяет вершины рёбрами попарно. Это делает нас “жителями двухполярной проекции”.
Парные отношения устойчивее.
В мире информации и физики два полюса легче стабилизировать, чем три. Система “А–Б” замыкается быстрее, чем триадная “А–В–С”. Поэтому вся техника, наука, язык фиксируют то, что проще наблюдать — пары, а не триады.
Двухполярность выгодна доминирующей культуре.
Бинарная логика удобна для выбора, контроля, решения: “кто прав — кто виноват”, “выключить — включить”. Трёхполярность требует удержания нескольких точек зрения одновременно, допуска неоднозначности. Это дороже и сложнее.
Что такое “наличие полярностей — фундамент пространства”
“Полярность” здесь — не физическая ось, а закон различимости, из которого строится пространство связей.
Двухполярность задаёт мир как набор противоположностей: поле и заряд, плюс и минус, субъект и объект.
Трёхполярность добавляет третий элемент — контекст, или замыкание, где две противоположности становятся соучастниками одного акта (☼).
Пример: наблюдатель–объект–среда, источник–проводник–приёмник, тезис–антитезис–синтез.
Именно из числа и типа этих “полярностей” рождается то, что мы называем “фундаментом пространства”: способ, каким пространство удерживает связи. Если носитель мира двухполярен, пространство — плоское, предметное, с фиксированными направлениями. Если трёхполярен, пространство становится актом замыкания, а не совокупностью линий; “прямая” и “кривая” перестают быть абсолютными, потому что связность определяется триадой, а не парой.
Почему мы воспринимаем реальность как плоскую
Наши приборы, язык и мышление создают двухполярную тень трёхполярного мира.
Это не ограничение Вселенной, это ограничение способа видеть:
мы измеряем по парам (координаты, векторы, отношения);
мы кодируем по парам (логика, компьютеры);
мы обучены решать по парам (причина–следствие).
Там, где в действительности происходит триадное замыкание (наблюдатель–среда–объект), мы видим только пару и говорим: “я вижу прямую связь”. Поэтому “мир кажется плоским” не геометрически, а структурно — по типу операций, которые мы допускаем.
Итог:
Мы живём не в “двухмерной вселенной”, а в мире, который нам видится двухполярным, потому что наши способы восприятия и описания фиксируют только парные отношения.
“Полярности” — это не координаты, а способы удержания различий.
“Фундамент пространства” — это закон, по которому различия соединяются.
А то, что трёхполярное замыкание для нас невидимо, — не “ахинея”, а констатация: часть связей реальности остаётся вне поля наших бинарных сенсоров.
Продолжение статьи: Иллюзия трёхмерного пространства: строгий анализ зрительного и тактильного восприятия