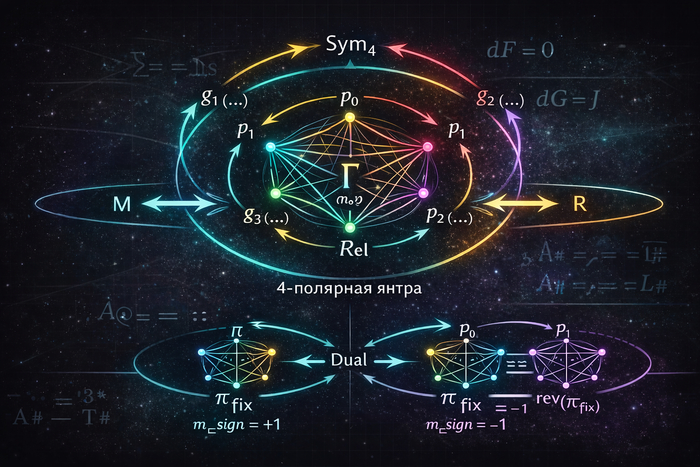
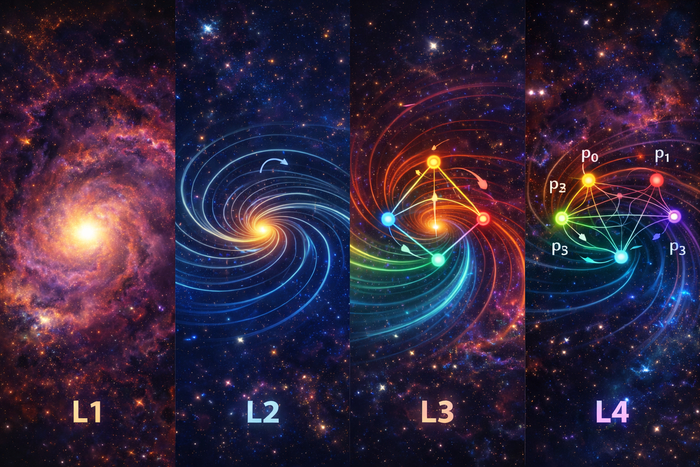
Интенсивности связи в двухполярности, трёхполярности и четырёхполярности
Янтра многополярности и «вихрь» как правило вычислимого обхода
Я задаю многополярность не метафорой, а конечной алгебраической конструкцией: есть конечное множество полярностей P и есть закон отношений, который на P определён полностью. Удобная форма такого закона — янтра: полная таблица бинарной операции.
1) Что такое универсальная янтра многополярности
Формально я фиксирую:
множество полярностей P (на уровнях L2/L3/L4 это |P|=2,3,4);
бинарную операцию *: P x P -> P, которая задаёт «что получается» при взаимодействии двух полярностей.
Если P конечное, операция полностью задаётся таблицей T[x][y] = x * y. Именно эта таблица (таблица Кэли конечной магмы) и есть янтра (термин введен В. Ленским) в строгом смысле: не «рисунок», а полное перечисление закона отношений.
Янтра многополярности (таблица Кэли конечной магмы). Подставляете n=3 — получаете три полярности; подставляете n=4 — четыре.
На практике я использую два слоя, которые не стоит смешивать:
Кадр (носитель) — способ нумерации полярностей, чаще всего как цикл Z_n: P ≅ Z_n = {0,1,...,n-1}.
Операция (собственно янтра) — таблица T, которая может быть:
«плюсовой» (в духе сложения по модулю как канонический изотропный каркас),
«звёздной» (в духе более жёсткого закона, несущего стоп/ремонт/поглощение и т.п.).
Именно разделение кадра и операции позволяет честно говорить о симметриях: часть преобразований — это просто перенумерация кадра, а часть — реальные автоморфизмы операции.
2) Зачем здесь симметрии и почему они не “украшение”
Как только P отождествлено с Z_n, возникает естественная группа перенумераций:
U_n (единицы по модулю n): x -> u*x (mod n),
и расширение Aff(n): x -> u*x + t (mod n).
Эта группа определяет классы эквивалентных представлений одного и того же закона отношений. Я принципиально рассматриваю симметрию не как эстетическую «красоту», а как инструмент:
канонизации (выбор нормальной формы таблицы/наблюдаемой),
факторизации перебора (орбиты вместо полного P^k),
контроля кадра (запрет скрытого смешения перенумераций).
Данная статья как раз использует симметрийную дисциплину, чтобы классификация интенсивностей связи была логичной.
3) Что такое «вихрь» в моей конструкции
«Вихрь» я понимаю не как картинку, а как правило обхода и оператор смены режима. Строго это означает следующее.
Я фиксирую, что эпизод (ситуация) предъявляется в форме тройки ролей K/A/P и проходит через вычислимую процедуру:
на L4 выполняются элементарные клеточные шаги вида X = A * P, Y = K * X, после чего включаются гейты (валидаторы) и решается вопрос: Outcome ∈ {PASS, BLOCK, REPAIR}.
на L3 выполняется замыкание тройки (фикс-пункт), то есть процедура, которая переводит тройку в устойчивое состояние относительно заданного правила (в терминах вычисления это итерация до стабилизации или до блока).
Вихрь — это именно композиция: L2 (турникет) -> L3 (замыкание) -> L4 (ориентация и дисциплина кадра).
Если дать одну формулу, то вихрь — это управляемое отображение Solve: E -> (E', Trace, Outcome), где Trace является обязательной трассой вычислений, а Outcome задаёт право продолжать или обязанность остановиться/ремонтировать.
4) Связь вихря с интенсивностями
Интенсивность связи в этой статье — это не “психологическая сила”, а весовая функция W(x,y) на кадре Z_n. Вихрь связывает её с вычислением так:
even-компонента интенсивностей отражает инвариантный фон (то, что не зависит от ориентации);
odd-компонента фиксирует ориентационный (вихревой) канал, который на L4 принципиально локализуется на соседних переходах и тем самым становится вычислительно дешёвым и контролируемым.
Дальнейшие три главы осуществляют следующий ход: фиксирут симметрийные аксиомы для W и выводят из них полную классификацию интенсивностей для L2, L3 и L4 — в виде параметрических нормформ, к которым невозможно придраться математически.
Глава 1. Каркас интенсивностей и строгая классификация для L2
1. Зачем вообще вводить «интенсивность связи» и как зафиксировать её математически
Я фиксирую «интенсивность связи» как ядро (kernel) на конечном множестве полярностей.
Пусть уровень многополярности задаёт носитель P = Z_n = {0,1,...,n-1}.
Интенсивность связи — это отображение W: P x P -> R, где R — упорядоченное множество интенсивностей (на практике достаточно R = R или R = Q; порядок нужен, чтобы формализовать «слабее/сильнее» без риторики).
Далее я фиксирую класс допустимых перенумераций (симметрий) как группу G, действующую на P. В рабочем каноне естественны две группы:
Автоморфизмы кадра (фиксирован ноль): U_n = { u in {0..n-1} : gcd(u,n)=1 }, действие: x -> u*x (mod n).
Аффинные перенумерации (кадровая калибровка допускается): Aff(n) = { (u,t) : u in U_n, t in Z_n }, действие: x -> u*x + t (mod n).
Симметрийный постулат для интенсивности формулируется жёстко:
(SYM-W) W(p(x), p(y)) = W(x,y) для всех p in G и всех x,y in P.
Это не «похоже/не похоже», а проверяемое равенство.
2. Орбитная нормформа: почему симметрия сжимает число параметров
Из (SYM-W) следует стандартная редукция: W обязана быть постоянной на орбитах действия G на P x P. Поэтому классификация W сводится к классификации орбит.
Самая полезная для вычислений версия — при G = Aff(n).
Лемма 1 (Aff-нормформа). Если W инвариантна относительно Aff(n), то существует функция k: Z_n -> R такая, что W(x,y) = k( (y - x) mod n ).
Смысл: перенос t убирает абсолютные позиции и оставляет только разность delta = y-x. Это и есть «жёсткая математическая упаковка» зависимости интенсивности от симметрии кадра.
Далее добавляется действие U_n на разности: delta -> u*delta. Тогда параметризация сжимается ещё сильнее: значения k(delta) должны совпадать на орбитах U_n в Z_n.
3. L2: полная и окончательная классификация интенсивностей
Теперь я перехожу к двухполярности.
На L2 носитель: P = Z_2 = {0,1}.
Разности: delta = (y-x) mod 2 принимают ровно два значения: 0 и 1.
Следовательно, при инвариантности относительно Aff(2) любая интенсивность имеет вид
W(x,y) = k(delta), где k(0) = a0, k(1) = a1.
То есть:
a0 — интенсивность самосвязи (диагональ),
a1 — интенсивность межполюсной связи (вне диагонали).
И это не «один из вариантов», а полная классификация:
Теорема 1 (классификация L2). Любое W: Z_2 x Z_2 -> R, инвариантное относительно Aff(2), однозначно задаётся парой (a0, a1).
Эквивалентно можно выписать матрицу:
W = [[a0, a1], [a1, a0]].
На L2 ничего третьего появиться не может без нарушения симметрийного постулата.
4. Зеркало и M-паритет: почему на L2 нет «вихревого» (знакового) канала
Я отдельно фиксирую зеркальное преобразование (то, что на L4 становится принципиальным):
m(x) = (-x) mod n.
Для n=2 получаем вырождение:
m(x) = x для всех x in Z_2.
Отсюда следует предельный результат:
Следствие 1 (вырождение M-нечётности на L2). Если попытаться ввести M-нечётную компоненту W_odd через требование W_odd(m(x), m(y)) = -W_odd(x,y), то на L2 неизбежно W_odd(x,y) = -W_odd(x,y), значит W_odd(x,y)=0 для всех пар.
Это важно: на L2 «интенсивность связи» не может нести устойчивой ориентации/знака, потому что зеркальный канал вырожден. Следовательно, на L2 остаётся только M-чётная (инвариантная) часть, полностью описываемая (a0,a1).
5. Как формально разместить «сложение (слабое) / умножение (сильное)» внутри L2
Фраза «сложение слабое, умножение сильное» становится корректной только после выбора правила сравнения интенсивностей. Я фиксирую сравнение как порядок в R.
Тогда «сложение» и «умножение» на L2 — это две разные функции интенсивности, например:
W_+(x,y) = (a0_plus, a1_plus), W_*(x,y) = (a0_star, a1_star),
где каждая из них обязана иметь L2-нормформу.
Строгое содержание фразы «умножение сильнее» можно задать так (без апелляций к вкусу):
Определение (сильнее по межполюсной связи). W_* сильнее W_+ по межполюсному каналу, если a1_star > a1_plus.
Определение (сильнее по контрасту). W_* сильнее W_+ по контрасту, если |a1_star - a0_star| > |a1_plus - a0_plus|.
Эти определения являются формальными и проверяемыми. Выбор одного из них — выбор физического/семантического смысла «силы связи». На L2 это всё равно всегда выбор между числами в паре (a0,a1); других степеней свободы симметрия не оставляет.
6. Итог главы 1: окончательная классификация L2
На L2 при симметрийной дисциплине кадра:
любая интенсивность связи является функцией delta = (y-x) mod 2;
существует ровно два независимых класса: delta=0 и delta=1;
любая такая связь полностью задаётся парой параметров (a0,a1);
M-нечётный (вихревой, знаковый) канал на L2 невозможен: он тождественно равен нулю.
В следующей главе я перейду к трехполярности (L3) и покажу, что там возникает минимальная невыражденная ориентация (разность 1 и 2 уже различаются через M-нечётность), а число параметров связи в симметрийной нормформе остаётся малым и вычислительно выгодным.
Глава 2. Трёхполярность: минимальная невыражденная ориентация и полный разбор интенсивностей L3
1. Носитель L3 и симметрийный класс, который фиксирует «право на канон»
На L3 я фиксирую носитель P = Z_3 = {0,1,2}
и работаю в той же математической дисциплине, что и на L2: интенсивность связи — это функция W: Z_3 x Z_3 -> R.
Далее я выбираю симметрийный класс перенумераций. Если в постановке допускается кадровая калибровка (перенос нуля), то естественная группа — аффинная: Aff(3) = { p_{u,t}(x) = u*x + t (mod 3) : u in U_3, t in Z_3 }, где U_3 = {1,2} (так как gcd(u,3)=1).
Инвариантность интенсивности задаётся тем же жёстким условием: W(p(x), p(y)) = W(x,y) для всех p in Aff(3) и всех x,y in Z_3.
Эта аксиома немедленно принуждает интенсивность зависеть только от разности.
2. Нормформа L3: зависимость только от delta
Определяю delta = (y - x) mod 3.
Лемма 2 (L3-нормформа по Aff(3)). Если W инвариантна относительно Aff(3), то существует k: Z_3 -> R, такое что W(x,y) = k(delta).
То есть все 9 значений матрицы связи сводятся к 3 значениям: k(0), k(1), k(2).
Однако на L3 присутствует дополнительная структурная закономерность: разности 1 и 2 связаны зеркалом.
3. Зеркало на L3 и разложение на M-чётную и M-нечётную части
Фиксирую зеркальное преобразование на кадре: m(x) = (-x) mod 3.
Тогда:
m(0)=0 (фикс-точка),
m(1)=2, m(2)=1 (обмен пары).
На уровне разности это означает: delta -> -delta (mod 3), то есть 1 <-> 2, а 0 остаётся 0.
Это даёт естественное разложение любой функции k(delta) на две компоненты: чётную и нечётную относительно delta -> -delta.
Определение (even/odd-разложение на Z_3). Для k: Z_3 -> R определяю:
k_even(delta) = (k(delta) + k(-delta))/2,
k_odd(delta) = (k(delta) - k(-delta))/2.
Тогда k = k_even + k_odd, и выполняются свойства:
k_even(-delta) = k_even(delta),
k_odd(-delta) = -k_odd(delta).
Для delta=0 это сразу даёт жёсткое ограничение: k_odd(0) = 0.
Итак, на L3 возникает то, чего на L2 не было: ненулевая M-нечётная (ориентационная) компонента возможна, но строго обязана менять знак при обращении направления.
4. Полная классификация интенсивностей L3 (в форме теоремы)
Теперь я фиксирую параметризацию.
Поскольку на Z_3 есть всего два типа разностей с учётом зеркала:
delta=0,
delta in {1,2} (обменная пара),
то M-чётная часть имеет два параметра:
k_even(0) = a0,
k_even(1) = k_even(2) = a1.
M-нечётная часть имеет один параметр (и обязана зануляться на 0):
k_odd(0)=0,
k_odd(1)= b,
k_odd(2)= -b.
Отсюда общий вид: k(0)=a0, k(1)=a1 + b, k(2)=a1 - b.
Теорема 2 (классификация L3-интенсивностей при Aff(3)). Любая интенсивность W: Z_3 x Z_3 -> R, инвариантная относительно Aff(3), однозначно задаётся тройкой параметров (a0, a1, b) и имеет вид W(x,y) = k((y-x) mod 3), где
k(0)=a0,
k(1)=a1 + b,
k(2)=a1 - b.
Эквивалентная матричная запись (в порядке индексов 0,1,2) такова:
W = [ [a0, a1+b, a1-b], [a1-b, a0, a1+b], [a1+b, a1-b, a0 ] ].
Эта форма является полной: других степеней свободы при заданной симметрийной дисциплине на L3 не существует.
5. Интерпретация «слабое/сильное» на L3 без размывания математики
На L3 корректно различаются два независимых механизма «силы»:
Фоновая (изотропная) связь: задаётся a1 (уровень связи между разными полюсами без ориентации). Это прямой аналог того, что на L2 выглядело как единственная межполюсная интенсивность a1.
Ориентационная (вихревая) добавка: задаётся b. Она не меняет симметрийный класс, но вводит направленный перекос: связь по delta=1 усиливается на +b, а по delta=2 ослабляется на -b.
Таким образом, строгая версия фразы «умножение сильнее сложения» на L3 может быть выражена двумя независимыми критериями (в зависимости от смысла «сильнее»):
по фону: a1_star > a1_plus;
по ориентации: |b_star| > |b_plus|.
Именно второй критерий является новым для L3: он невозможен на L2, потому что там M-нечётная компонента вырождена.
6. Роль L3 в “замыкании”: почему триадная структура соответствует минимальной локализации
На уровне интенсивностей L3 фиксирует минимальный невыражденный цикл. С точки зрения вычислительной процедуры это означает:
есть замкнутый носитель Z_3, на котором направленность (b) не является произволом; она обязана быть антисимметричной относительно зеркала;
эта направленность вводит строго различимый «ход» по циклу (один шаг вперёд и один шаг назад различаются по интенсивности).
В терминах ядра это соответствует тому, что L3 уже способен задавать локальную согласованность не через эвристику, а через два канала: фон и ориентацию.
Итог главы 2 (в одной связке)
На L3 при симметрийной дисциплине Aff(3) интенсивность связи имеет ровно три независимые компоненты:
a0 (самосвязь, delta=0),
a1 (изотропная межполюсная связь, delta=1/2 без ориентации),
b (ориентационная M-нечётная добавка, различающая delta=1 и delta=2).
Именно b является минимальным математическим носителем «вихря» на L3: он строго определён как антисимметричная часть относительно зеркала и не допускает произвольных “подмен кадра” при сохранении заданных симметрий.
В следующей главе я перейду к четырехполярности (L4) и покажу, что там классификация становится богаче (появляется отдельный класс delta=2 как “противоположность”), а вихрь приобретает принципиально жёсткую локализацию: M-нечётная часть вынужденно зануляется на фикс-разностях и живёт только на соседних переходах.
Глава 3. Четырёхполярность: три класса расстояний, вихрь на соседях и итоговая классификация L4
1. Носитель L4 и симметрийный режим, в котором классификация становится жёсткой
На L4 я фиксирую P = Z_4 = {0,1,2,3}
и интенсивность связи W: Z_4 x Z_4 -> R.
Как и раньше, я принимаю симметрийную дисциплину кадра: если допускается кадровая калибровка, то группа перенумераций Aff(4) = { p_{u,t}(x) = u*x + t (mod 4) : u in U_4, t in Z_4 }, где U_4 = {1,3} (единицы по mod 4), то есть u = +1 или u = -1 (mod 4).
Инвариантность формулируется жёстко: W(p(x), p(y)) = W(x,y) для всех p in Aff(4).
2. Нормформа L4: зависимость от разности и распад на классы delta
Определяю разность: delta = (y - x) mod 4.
Лемма 3 (L4-нормформа по Aff(4)). Если W инвариантна относительно Aff(4), то существует k: Z_4 -> R такое, что W(x,y) = k(delta).
В отличие от L3 здесь появляется принципиальный новый элемент: разности распадаются на три симметрийно различимых типа:
delta = 0 (самосвязь),
delta = 2 (противоположность),
delta in {1,3} (соседи, зеркальная пара).
Это и есть математический источник того, что на L4 у интенсивностей появляется больше классов, чем на L2/L3.
3. Зеркало на L4: две фикс-точки и жёсткая локализация вихря
Зеркало на кадре: m(x) = (-x) mod 4.
На Z_4 оно имеет две фикс-точки: m(0)=0, m(2)=2, и меняет местами соседей: m(1)=3, m(3)=1.
На уровне разностей это означает: delta -> -delta (mod 4), то есть 0 -> 0, 2 -> 2, 1 <-> 3.
Отсюда следует ключевой вывод для M-нечётной части:
Следствие 2 (нули odd-канала на фикс-разностях). Если k_odd(-delta) = -k_odd(delta), то при delta = -delta (mod 4) имею k_odd(delta) = -k_odd(delta), значит k_odd(delta)=0.
Для Z_4 это означает: k_odd(0)=0 и k_odd(2)=0.
Итак, вихревое (ориентационное) отклонение на L4 не может сидеть ни на самосвязи, ни на связи с «противоположностью». Оно может жить только на соседних переходах delta=1 и delta=3.
Это структурный факт, из которого следует вычислительная экономия и дисциплина “видимости знака”.
4. Полная классификация интенсивностей L4 (в форме теоремы)
Теперь я фиксирую параметризацию.
4.1. M-чётная (even) часть
Поскольку k_even(-delta)=k_even(delta), имею независимые классы:
delta=0: k_even(0)=a0,
delta=2: k_even(2)=a2,
delta=1 и delta=3: k_even(1)=k_even(3)=a1.
Итого три even-параметра: a0, a1, a2.
4.2. M-нечётная (odd) часть
По следствию выше:
k_odd(0)=0,
k_odd(2)=0,
k_odd(1)=b,
k_odd(3)=-b.
Итого один odd-параметр: b.
4.3. Общий вид
Значит:
k(0) = a0,
k(2) = a2,
k(1) = a1 + b,
k(3) = a1 - b.
Теорема 3 (классификация L4-интенсивностей при Aff(4)). Любая интенсивность W: Z_4 x Z_4 -> R, инвариантная относительно Aff(4), однозначно задаётся четвёркой параметров (a0, a1, a2, b) и имеет вид W(x,y) = k((y-x) mod 4), где
k(0)=a0,
k(2)=a2,
k(1)=a1 + b,
k(3)=a1 - b.
Эквивалентная матричная форма (индексы 0,1,2,3) такова:
W = [ [a0, a1+b, a2, a1-b], [a1-b, a0, a1+b, a2 ], [a2, a1-b, a0, a1+b], [a1+b, a2, a1-b, a0 ] ].
Эта форма полна: других степеней свободы при (SYM-W) для Aff(4) не существует.
5. Итоговая классификация связей L2/L3/L4 в одной таблице параметров (без “табличной эстетики”)
Я фиксирую общий принцип:
интенсивность в симметрийном режиме Aff(n) всегда есть функция разности delta;
далее она распадается на even/odd части относительно delta -> -delta;
odd-часть обязана зануляться на фикс-разностях зеркала.
Отсюда получается минимальный набор параметров:
L2 (n=2): (a0, a1) (odd-канал вырожден).
L3 (n=3): (a0, a1, b) (odd живёт на паре delta=1/2 как +b/-b).
L4 (n=4): (a0, a1, a2, b) (even распадается на 0, 2, ±1; odd живёт только на ±1).
Это и есть «жёсткая итоговая классификация», в которой нет ни одного места для риторического спора: она полностью выводится из (SYM-W) и структуры зеркала на Z_n.
6. Как из этой классификации следует «слабое сложение / сильное умножение» на L3 и L4
Если на L2 я мог отождествить «сложение» и «умножение» с двумя разными наборами параметров (a0,a1), то на L3 и L4 картина становится богаче:
«слабое» естественно связывается с изотропным even-фоном (b=0), потому что он не вводит ориентации и не ломает зеркальную симметрию.
«сильное» связывается с включением вихря (|b|>0), то есть с появлением устойчивого направленного перекоса, который на L4 ещё и локализован строго на соседях.
Если дополнительно вводится смысл “сильнее = сильнее связывает противоположность”, то на L4 появляется ещё один независимый рычаг: параметр a2.
Таким образом, в терминах строгой параметризации:
L3: «усиление» может означать рост a1 (фон) и/или рост |b| (ориентация).
L4: «усиление» может означать рост a1 (соседи), рост a2 (противоположность) и/или рост |b| (вихрь на соседях).
7. Финальный вывод статьи
Я получил не интерпретацию, а классификацию.
В симметрийной дисциплине Aff(n) интенсивность связи на Z_n неизбежно является функцией разности delta=(y-x) mod n.
На L2 это даёт ровно два класса (самосвязь и межполюсная связь) и исключает вихревой канал.
На L3 появляется минимальная невыражденная ориентация: odd-компонента различает два направления цикла.
На L4 even-компонента распадается на три класса (0, 2, ±1), а odd-компонента вынужденно зануляется на фикс-разностях и живёт только на соседних переходах.
Эта структура и есть математическое ядро тезиса: «интенсивности связи» в многополярности не придумываются произвольно, а выводятся из симметрий кадра и зеркального разложения even/odd.
Как повторить
Текст статьи подготовлен с использованием ChatGPT. Однако он опирается на архив проекта, в котором зафиксированы структура многополярности (единый граф), протокол запуска и контрольные процедуры (гейты), обеспечивающие воспроизводимость и логическую дисциплину.
Скачайте архив MP_YANTRA_CORE_iter063.zip, загрузите его в первое сообщение чата ChatGPT и напишите:
«Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива».
Дальше задавайте любые вопросы по многополярности (в пределах двухполярности L2, трехполярности L3, четырехполярности L4).
Смысл "на пальцах" этой статьи изложен здесь
Читайте также:
\О твёрдом фундаменте многополярной математики, или Почему многополярность не поддаётся приватизации